GF (q) и используется для декодирования кодовых слов длины Я кода . Щ

Хотя для односторонних каналов связи без памяти использование тензорного произведения не представляется особо привлекательным, Вулф [1965 а] показал, что некоторые коды такого сорта позволяют исправлять кратные пакеты ошибок. Элспас и Вулф [1963] и Вулф j [1965 Ы построили тензорные произведения кодов, которые могут быть использованы для локализации искаихснных подблоков. При использовании таких кодов в двухпутевых каналах связи приемник может запрашивать передатчик о ретрансляции только искажен- ных подблоков.

14.86. Прямая сумма кодов. Если Л ш - коды над одним и тем ;ке полем, то прямой суммой Л @ называется код, состояш,ий из всех слов вида а * Ь, где а 6 Л, 6 6 а * обозначает композицию ). Длина кода Л @ равна сумме длин кодов Л и , а его размерность - сумме размерностей этих кодов; минимальное расстояние кода Л + равно наименьшему из минимальных расстояний кодов Л ж .

Хотя прямая сумма кодов мало схожа с прямым произведением кодов, вместе эти два понятия употребляются очень часто.

Код 3) называется разложимым, если после некоторой перестановки координат он люжет быть записан в виде прямой суммы ё = = А @ . Слепян [1960] показал, что ни один разложимый линейный код не имеет большее минимальное расстояние или меньшую вероятность ошибки, чем лучший неразложимый линейный код с той же скоростью и блоковой длиной.

14.9. Каскадные коды

Если прямое произведение кодов кодируется и декодируется каскадным образом, как показано на рис. 14.2, то такая система

Внешний канал

Получатель

данных

Рис. 14.5. Система с каскадным кодированием и декодированием.

передачи является частным случаем системы, представленной на рис. 14.5 и исследованной впервые Форни [19б6 Ы. Этот раздел представляет собой краткое введение в работу Форни.

1) Действия над словами я*Ь производятся так: а*Ъ ai*bi = (а -\- Oi)* *(6 -- bi), Я (а*Ъ) = Ха*ХЬ (Я - элемент поля).- Прим. ред.

Предположим, что устройства внутреннего кодера и внутреннего декодера, выделенных на рис. 14.5, заданы заранее и фиксированы, и остановимся на задаче выбора внешних кодера и декодера, улучшающих характеристики их выходного капала.

Внутренний кодер разбивает поток поступающих данных на блоки 110 к символов и кодирует калдый из этих блоков более длинными блоками по п символов. Блок длины п передается затем по виутрен-тюму каналу и декодируется во внутреннем декодере. Поток данных, поступающих на выход внутреннего декодера, состоит из блоков по к символов, представляющих собой информационные символы декоди-))уемых блоков длины п. Хотя ошибки внутри одного такого блока статистически не зависят от ошибок в других блоках, в пределах одного блока они статистически зависимы. Большинство декодируемых блоков длины п вообще не будет содержать искаженных симво-.-ов, но немногие пораженные блоки скорее всего будут содержать несколько искаженных позиций.

Ошибки внутри любого блока длины п должны составлять кодовое слово. Предположим, например, что в качестве внутреннего кода используется регистровый код максимального периода с блоковой длиной п = 2 - 1. Этот код эквидистантен, и вес всех его ненулевых слов равен 2-. Следовательно, если в декодируемом блоке из п символов искажена любая позиция, то он содержит точно 2" иска-;1;енных символов. В силу эквидистантности кода вектор ошибок в пределах к информационных символов с равной вероятностью принимает любое жз 2 - 1 возможных ненулевых значений. Другими словами, каждый из блоков по к информационных символов, передаваемых от внутреннего декодера к внешнему, либо полностью не искажен, либо полностью случаен.

В силу этих причин внешний декодер может рассматривать каж-,11.1Й поступающий к нему блок из к символов как одну букву выходного алфавита порядка 2**. Если внутренний код эквидистантен, то все ошибки в этом внешнем алфавите равновероятны.

В общем случае, если внутренний код содержит к информацион-m.ix символов в блоке над GF (д), то можно рассматривать внутренний кодер, внутренний канал и внутренний декодер как единый внешний канал, входные и выходные элементы которого нрипад.лежат алфавиту порядка = д. Выходной канал не имеет памяти. 1> общем случае вероятности переходов символов в друг друга вычислить трудно, так что удобно полагать, что внешний код подобран так, что все искажения символов равновероятны. Будем считать, что пиешлий код - код над GF (д) с метрикой Хэмминга.

Так как достаточно велико, то в качестве выходного кода мож о выбрать код Рида - Соломона (РС-код). Из результатов разд. 13.3 известно, что РС-код имеет наибольшее минимальное расстояние среди всех линейных кодов с той же скоростью и той же блоковой .(липой. В гл. 10 было показано, что к РС-кодам, как и ко всем

БЧХ-1£0дам, применимы эффективные алгебраические методы коди-j рования и декодирования.

Взятые вместе, РС-код над GF (q) и внутренний код над GF (gj)! образуют очень длинный каскадный суперкод над GF (qj). Скорость! передачи информации такого суперкода равна произведению скоро-] стей РС-кода и внутреннего кода.

Для построения каскадного суперкода со скоростью R и длиной N\ над GF (gi) надо соответствующим образом выбрать блоковую длину! и скорость внутреннего кода и построить этот код. Для целей анали-1 за можно взять случайно выбранный внутренний код. Даже если для декодирования такого кода придется использовать перебор всех! gj кодовых слов, то по сравнению с длиной Л суперкода это количе-! ство вычислений не является чрезмерным. Если к - алгебраическая! функция от log то количество вычислений на декодируемый блок! внутреннего кода будет алгебраической функцией от N. Число вычис- лений на суперблок относительно внутреннего декодера - степен-j пая функция от Л, и, конечно, общее число вычислений на суперблок,) необходимое для декодирования РС-кода, также степенная функ- ция от Л.

Вычисление вероятности ошибки декодирования на суперблок,] т. е. вероятности того, что каскадный декодер не сможет правильно! декодировать все информационные символы суперблока, зависит! как от вида границ для вероятности ошибки случайного кода, так и от частного выбора скоростей и блоковых длин для внутреннего! и внешнего кодов. Форни [1966b] получил очень интересный ре- зультат, согласно которому для всех скоростей, меньших пропу-1 скной способности канала, вероятность ошибки декодирования! на блок стремится экспоненциально к нулю с ростом длины N с упер-j блока.

Форни [1966b] вычислил также характеристики системы, в кото- рой внутренний декодер может передавать выходному декодеру! некоторые дополнительные сведения. Улучшение экспоненты вероят- ности ошибки при каскадном декодировании можно получить, есл1 позволить внутреннему декодеру передавать выходному декодеру, помимо каждого декодируемого блока, оценку вероятности его1 правильного декодирования. Если такую оценку не передавать, то максимальная экспонента каскадного декодирования уменьшается! вдвое. Если внутренний декодер не передает оценки вероятности! правильного декодирования, но стирает все неоднозначные внутрен-! ние блоки, то общая экспонента составляет две трети от максимально! достижимой.

Читателя, заинтересованного в более подробном изучении каскад-1 ных кодов, мы отошлем к монографии Форни [1968].

Каскадные коды Форни и итеративные коды Элайеса не являются! единственно известными методами построения реализуемых систем! связи, сложность декодирования в которых растет сравнительнс

медленно с ростом блоковой длины. Эпштейн [1958а1 предложил такую систему для двоичного канала со стиранием; Хорстейн [1963], Берлекэмп [1964а[ и Шелквик с Кейласом [19661 построили такие системы для каналов с бесшумной обратной связью. Возенкрафт и Рейффен 1) [1961], Фано i) [1963], Галлагер [1963[, Зив [1962, lJ66, 1967], Пинскер ) [1968[ и Фэлконер [1967] предложили такие системы для каналов без обратной связи и без стирания.

См. разд. 15.65.

Глава 15

Другие основные методы кодирования и декодирования

15.1. Коды Сривэставы - нециклические коды алгоритмом декодирования

с алгебраическим!

Как было показано в разд. 10.1, в качестве локаторов кода над! GF (д) удобно взять элементы поля GF (д). При этом задача декоди-j роваиия сводится к отысканию минимального множества локаторов! ошибок Zj, Х2, . . ., Хе [Xi 6 GP(g™)] и соответствуюш,еГо множества! величии ошибок Fj, Уз, . . .,Уе [У; g GF (q)], удовлетворяюш,их npo-l верочным соотношениям. Для БЧХ-кодов более удобным оказывается! не непосредственный поиск множеств {X} и {У}, а отыскание много-] члена локаторов ошибок

(15.11)

o(z)-U{i-XiZ)

и многочлена значений ошибок (15.12) l{z) = YiXillii-Xjz).

Степень многочлена (15.12) всегда жнъше числа ошибок. Используя; формулы (15.11) и (15.12), получаем, что

(15.13)

0(2)

Сривэстава [1967] предложил класс линейных кодов, задаваемых [ проверочной матрицей вида

(15.14)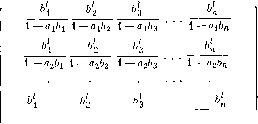

где I - некоторое целое число, а, а, • , aa-i - различные элементы поля GF (д") и Ь, Ъ, . . ., 6„ - элементы множества

GF (д"") \ (О, а7\ а~, aj\ . . ., a-i}- Блоковая длина кода равна (f - d. Проверочные соотношения кода Сривэставы связаны с уравнением (15.13). Они определяют величины [o-illo (ад для i = - 1, 2, . . ., d - 1. Задача декодера состоит в определении мпого-члепов (z) и 0 (z) по этим известным величинам. При deg •< < deg а (d - 1)/2 суш,ествует не бо.тее одной пары многочленов а (z) и I (z), удовлетворяющих этим условиям. В самом деле, если существует и другое решение [б (z), ср (z)], то для i = i, 2, . . ., d - i

(15.15)

б (fli) I {at) - о {ад ф (at) = 0.

Согласно теореме 2.15, любой многочлен степени <й - 1, обладающий d - 1 корнями, есть тождественный нуль. Так как deg (б - оф) <;d - 1, то из (15.15) вытекает, что (z)/a (z) = = ф (z)/6 (z). В силу взаимной простоты многочленов (z) и а (z) это означает, что существует пе более одной пары многочленов Ь, (z) и о (z), таких, что deg g < deg о (d - 1)/2, при заданных значениях (аг)/о («;) (J = l, 2, . . ., d- 1) . Следовательно, код с проверочной матрицей (15.14) исправляет любые комбинации из (d - 1)/2 ошибок. Читатель легко может проверить, что минимальное расстояние кода равно но меньшей мере d.

Берлекэмп [19671 предложил эффективный метод декодирования кодов Сривэставы, основанный на использовании последовательности многочленов, сходящихся к а (z) и g (z). Можно также построить эффективную процедуру декодирования, основанную на численном методе отделимых разностей, описанном Милном [19491. Любой из подходов приводит к декодированию, которое в случае длинных кодов Сривэставы лишь незначительно сложнее, чем для сравнимых БЧХ-кодов.

При I = 1 двоичные коды Сривэставы с проверочной матрицей (15.14) на самом деле исправляют d - I ошибок. В двоичном случае все ненулевые значения У равны 1 и уравнение (15.12) записывается

в виде 1 (z) = о (z) = о {z)lz [здесь о (z) - производная от о (z)

по Z, а 0 (z)- нечетная часть о (z)[. Проверочные соотношения тогда

дают значения о (z) = z о (z) в точках z = а, а,, . . ., Ud-i. Эти условия определяют не более одного многочлена локаторов ошибок степени < d - 1. Если существуют два таких многочлена о (z) и б (z), то

(15.16) откуда (15.17)

о (at)

б (at)

atlS (aO + ff (ai)] at [6 (яг) + 6(яг)] a (a;) б (a,) б (ai)CT (a,)