
 |
|
Главная страница Алгебраическая теория кодирования [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [ 57 ] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] 14.821. Т е О р е м а (Бартон - Велдон ([1965]). Если iPi + Н2Р2 = 1 niod П1П2, Jh - циклический код с длиной щ и порождающим многочленом а {х), 3S - циклический код с длиной и порождающим многочленом Ъ {х), то циклически упорядоченное прямое произведение кодов Ли У. 3S является циклическим кодом с длиной П1П2 и порождающим многочленом g (х) = н. о. д. (а (хР2"2) ь (хР1"1), х"1"2 - 1). Доказательство. Согласно Элспасу [1968], компоненты двумерного кодового слова С можно представить как коэффициенты многочлена от двух переменных: С{х,у)= S С,-.,-хУ. 1=0 j=o С другой стороны, компоненты С можно рассматривать как коэффициенты многочлена от одной переменной: П1П2-1 C(z)= S Ciz\ где Ci и Ci,j связаны правилами (14.811) циклического упорядочения. Пусть а - примитивный корень {щп-ш степени из единицы; Р = а"2 и Y = а"!. Тогда эквивалентны следующие утверждения: 14.822. С 6 X 14.823. а (х) Ъ (у) С (х, у). 14.824. Из а ф) b (у) = О следует, что С (р у) = 0. 14.825. Из g (PV) = О следует, что С фу) = 0. 14.826. g{z)\C (2). Эквивалентность утверждений 14.822 и 14.823 следует из определения 14.812. Утверждения 14.823 и 14.824 эквивалентны потому, что каждый корень многочлена а (х) является степенью р, а каждый корень многочлена b (у) есть степень 7. Если I определено соотношениями (14.811), то Ип2 + jJn = 11п2 + IJn mod П1П2. Имеем П1П2- 1 i 3 Таким образом, (14.827) C(P7j) = C(PV)-Согласно определению g{x), (14.828) e(PV) = «(POb(/)- Эквивалентность утверждений 14.824 и 14.825 следует из равенств (14.827) и (14.828). Наконец, эквивалентность утверждений 14.825 и 14.826 вытекает из того факта, что каждый корень многочлена g (х) является корнем {п1П2)-ш степени из единицы, а каждый корень (иДа)" степени из единицы может быть записан в виде Ру-, где I я J - подходящим образом подобранные целые числа, щ 14.829. Следствие. В условиях теоремы 14.821 g{x)u.o.к.{d{xrг),f{xn)), d (х) = н. о. д. (а (а;Р2), - 1), /(х) = н. о. д. {Ь (xPi), Х"2 1). Доказательство. п. о. к. (d (Р"2уп2) f ф1пп1)) а (Р) b (у). I Пусть 3 и ff - циклические коды с порождающими многочленами d (х) и f (х). Согласно результатам разд. 5.8, 3 и являются перестановками А ж следовательно, deg d (х) = deg а (х) и deg / (х) = deg b (х). Поскольку циклическое упорядочение отличается от канонического, то декодер для циклического произведения кодов несколько отличается от каскадного декодера, изображенного на рис. 14.2. Так как из канала связи символы поступают в последовательности Соо, Со,п1, Со, 2п1, . . ., то, как заметил Эбрамсон [1968], на первом этапе каскадного декодера должен использоваться декодер для кода в котором единичные элементы задержки заменены линиями задержки из элементов, а на втором этапе каскадного декодера - декодер для кода 3, в котором каждая единичная задержка заменена линией задержки из «2 элементов. Теорема 14.821 и следствие 14.829 позволяют определить, можно ли заданный код с блоковой длиной иПз представить в виде произведения двух циклических кодов с длинами п и Для этого надо выписать все корни исходного порождающего многочлена в виде набора пар (/, /) и проверить выполнение условий теоремы 14.821 и следствия 14.829. Многие неразложимые коды являются подкодами больших кодов, которые разложимы в произведение циклических кодов. Эта задача о разложении изучалась с более абстрактной точки зрения Гёталсом [1967]. 14.83. Среднее число ошибочно декодируемых символов в коде Хэмминга. Чтобы рассчитать характеристики прямого произведения кода Хэмминга и некоторого другого кода, полезно прежде найти среднее число ошибочно декодируемых символов в 1-удлиненном коде Хэмминга с блоковой дли- ной 2™ при передаче по двоичному симметричному каналу без памяти с вероятностью Р ошибки в одном символе. Если в канале искажается четное число символов блока длины 2"*, то декодер для кода Хэмминга не изменяет принятого вектора; если число ошибок нечетно, то декодер изменяет один символ на противоположный. Если в канале произошла только одна ошибка, то она будет исправлена. Однако, если ошибок несколько, то декодер либо исправит одну из них, либо внесет новую ошибку. Декодер исправит ошибку тогда и только тогда, когда вес вектора ошибок равен i + 1 и он находится на расстоянии 1 от кодового слова веса i; декодер внесет дополнительную ошибку тогда и только тогда, когда вес вектора ошибок равен i - 1 и вектор находится на расстоянии 1 от кодового слова веса i. Обозначим через Л"" число кодовых слов веса i в 1-удлиненном коде Хэмминга с длиной 2", и пусть Л<") (г) = ] A\z\ Среди 2"" слов, расположенных на расстоянии 1 от данного кодового слова веса i, точно i слов имеют вес i - 1 и точно 2" - i слов имеют вес i + 1. Следовательно, нумератор ошибок, приводящих декодер к дополнительной ошибке, равен 2 iATh = zA (z), а нумератор исправляемых декодером ошибок равен 2 (2*"- О i""z* = 2".4™> (z)- - zA" (z). Если вероятность ошибки в канале равна Р, то среднее число 1 ошибок равно е = 2Р. Вероятность того, что декодер внесет допол- 1 Согласно (14.832), при 2,1779;<е < 2" более вероятно, что декодер внесет дополнительную ошибку, чем исправит происшедшую ошибку. нительную ошибку, равна 2 iAP (1 - Pf ~ = (1 - Р) {)г где X = Р/{1 -Р). Аналогично, вероятность исправления ошибки равна (1 - Р)" X [2™Л""> (х) - хЛ" (х)]. Используя эти вероятности, можно вычислить 8 - среднее число искаженных символов в принятом блоке. Соответствующая формула имеет вид (Ц.831) 8 = e-(l-e2-")2"[2"(»)(a;)-2a;<">(a:)], где X = е2-"/(1 - 62-"). Формула для Л С") (z) будет выведена в разд. 16.2. Мы не приводим здесь этого вывода, поскольку не хотим отвлекать читателя громоздкими деталями доказательства. Функциональное соотношение между е и е зависит от т, при m оо существует предельное соотношение, график которого изображен на рис. 14.3. Две точки этой кривой заслуживают особого внимания: если е< 2,1779; (14.832) (14.833) 8<е, в<4 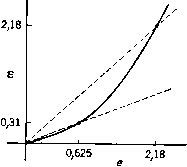 если е<; 0,6246. Рис. 14.3. Соотношение между средним числом искаженных символов в блоке до и после декодирования для длинных 1-удлиненных двоичных кодов Хэмминга. Это не должно быть слишком удивительным, так как декодер, исправляющий одиночные ошибки, будет декодировать любой вектор ошибок веса 3 в кодовое слово веса 4. 14.84. Коды Элайеса. Конструкция прямого произведения кодов легко распространяется на любое число множителей. Например, прямое произведение кодов Л, 3S ъ % определяется как {Л У. Щ у.%. Следуя замечательной идее Элайеса [1954], рассмотрим прямое произведение 1-удлиненных двоичных кодов Хэмминга с блоковыми длинами 2, 2+1, 2+2, .... Так как скорость прямого произведения равна произведению скоростей сомножителей, то для бесконечного произведения 1-удлиненных кодов Хэмминга получаем i?,= II [l-(m-f 1)2-]. Ясно, что это произведение сходится к положительному пределу, так как Примерные значения скоростей таковы: Ло = 0,92- i?, = О 86-/?в = 0,77; R, = 0,63; R, = 0,43; R, = 0,21; R, = 0,05. Бесконечный каскадный декодер для бесконечного прямого произведения показан на рис. 14.4. На первом этапе такого декодера используется декодер для 1-удлиненного кода Хэмминга с блоковой длиной 2\ на втором этапе - декодер для 1-удлиненного кода Хэмминга с блоковой длиной 2*, .... Пусть 8 - среднее число искаженных символов в блоке, поступающем на вход декодера для кода Хэмминга с длиной 2"*. Тогда нероятность ошибки в символе равна 8/2", и среднее число ошибок в блоке длины 2"+ равно em+i = 2"+ism/2" = 28. Эти ошибки не являются статистически независимыми, так как в пределах любого блока 1-удлиненного блока кода Хэмминга с длиной 2 содержится четное число искаженных символов. Более того, иногда эти ошибки образуют кодовые слова. Однако ошибки внутри одного блока статистически независимы от ошибок, расположенных внутри другого Канал декодер для кода Хзмминеа Декодер для кода Хзшинга длины г* с заменой элементов единичной, задержки на. линии из Z элементов единичной задержки Декодер для кода Хэмминга длины г*сза-меной злементов единичной эадерж ки на линии из 2* злементов единичной задержки Декодер для кода Хэмминга длины г" с заменой элементов единичной задержки на линии из элементов единичной задержки Рис. 14.4. Каскадный декодер для кода Элайеса, блока кода. Следовательно, ошибки, расположенные внутри блока из 2""+ символов, поступающего на вход декодера следующего кода Хэмминга, статистически независимы. Это позволяет использовать равенство (14.831) для расчета вероятности ошибки в символе на каждом этапе каскадного декодера. В силу свойства (14.833) заключаем, что если е < 0,6246 для любого достаточно большого т, то e+i = 28„ <е. В этом случае среднее число ошибок на декодируемый блок уменьшается на каждом этапе каскадного кода не менее чем в 2 раза. Поэтому хотя блоковый «объем» соответствующих кодов Хэмминга увеличивается, среднее число ошибок на блок стремится к нулю. С другой стороны, если 0,6246 < ет для достаточно большого т, то e+i > и 6>m-n <ет-ь2 <m+3- • . • В конце КОНЦОВ МЫ найдем такое к, что е+А > 2,1779. После этого любые дальнейшие попытки декодирования будут приводить лишь к увеличению среднего числа ошибок в блоке. Таким образом, для достаточно больших т величина 0,6246 является критической точкой для е- На основе равенства (14.831) с помощью вычислительного устройства нами получены следующие! критические значения:
Как видно из этой таблицы, каскадный декодер для бесконечного прямого произведения 1-удлиненных кодов Хэмминга длин 2*, 2, ... обеспечивает безошибочное декодирование, если вероятность ошибки в символе в канале не превосходит 0,0402. Если Р = 0,0402, то вероятность ошибки в каждом символе после соответствующего блока каскадного декодера становится равной 0,0192, 0,00983, .... Коды Элайеса - единственный известный класс кодов, обеспечивающих безошибочное кодирование в одностороннем двоичном симметричном канале с положительной скоростью передачи. 14.85. Тензорное произведение кодов. Любая проверочная матрица из г строк и п столбцов над GF (д™) может быть продолжена до проверочной матрицы из тг строк и п столбцов над GF (д), как это сделано в примере (5.21) на стр. 134 для г = 2, g = 2, пг = 4 и и = 15. Соответствующий код над GF (д) будем называть продолжением кода над GF (д"*), а код над GF (д™) будем называть сжатием кода над GF [q). Каждый код над GF (g™) имеет единственное продолжение, но некоторые коды над GF (д) имеют несколько сжатий на GF (д™), в частности, если избыточность кода hajiGF (g) не кратна т. Если и - коды над GF (д"*) и .-продолжение кода ё над GF (q), то тензорным произведением называется продолжение кода, дуального к прямому произведению дуальных Л -л кодов. Если длина и избыточность кода А равны п и г, а длина и избыточность кода равны п и г2, то длина и избыточность кода .з® равны пп и rjA-g. Практически часто для кода ё полагают = т, а в качестве А выбирается код Рида - Соломона. В декодере сначала декодируется код А, причем гт символов синдрома над GF (д) рассматриваются как символов синдрома над GF (д"*), а полученные «значения ошибок» лежат в GF (д"*). Каждое из этих «значений ошибок» рассматривается затем как Га-символьный синдромнад [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [ 57 ] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] 0.0121 |