
 |
|
Главная страница Алгебраическая теория кодирования [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [ 56 ] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] минимальным расстоянием 10 и порождающей матрицей "0 10011100111001101110 (14.24) 100101001110011011101 001010011110110111010 010110111110101110101 101101111101011101010 Используя границу Грисмера, Соломон и Стиффлер показали что каждый линейный код, полученный выбрасыванием подпрост- ранств различных размерностей из регистрового кода максимально! длины, является оптимальным в том смысле, что никакой линейны! код с тем же числом кодовых слов и тем же минимальным расстоя- пнем не может иметь меньшую блоковую длину. Процедура 1-укорочения, предложенная Соломоном и Стиффле ром, позволяет построить многие оптимальные коды, но в силу orpa-j ничения (14.22) все эти коды обладают малой скоростью или мало блоковой длиной. 14.3. Присоединение дополнительных кодовых слов Циклический код, порожденный многочленом g (х), может быт] расширен до циклического кода с той же блоковой длиной, порождав ющий многочлен которого делит многочлен g (х). Наиболее часто встречается расширение циклического кода путем перехода к кодл спорождающим многочленом g {х)1{х - 1) (см. рис. 14.1). В соответствии с границей Гилберта (лемма 13.72 и теорема 13.73 и известными асимптотическими свойствами БЧХ-кодов (разд. 12.7 к любому достаточно длинному БЧХ-коду со средней скорость! можно присоединить много кодовых слов, не изменяя его минималИ ного расстояния. К сожалению, решительно ничего не извести о том, как находить эти дополнительные кодовые слова. 14.4. Выбрасывание кодовых слов Любой циклический код, порожденный многочленом g {х), може быть сужен до циклического кода путем умножения порождаг щего многочлена g {х) на дополнительный множитель. Наиболе распространенное сужение дает переход от g (х) к g {х) (х - 1)1 В двоичном случае при этом получаем подкод, состоящий из всез слов четного веса исходного кода. Часто минимальный вес сужен- ного кода на единицу больше минимального веса исходного кода однако возможны случаи, когда минимальный вес суженного код сохраняется или превосходит минимальный вес исходного кода боле чем на 1. Все эти случаи можно проследить на двоичном циклической коде с блоковой длиной 15, веса которого приведены в табл. 16.1 Шеннон [1959] и Галлагер [1965] исследовали границы надежности (см. разд. 13.8) при выбрасывании кодовых слов достаточно малого веса из случайно выбранного кода. При малых скоростях эта граница - одна из лучших известных, а при нулевой скорости она является точной. Подобно методу расширения кодов, который также очень полезен при неконструктивном исследовании границ, метод сужения кодов за исключением тривиальных случаев не может быть конструктивно использован в алгебраической теории кодов. 14.5. 2-удлинение кодов (добавление информационных символов) Если порождающий многочлен двоичного циклического кода с блоковой длиной п содержит множитель а; + 1, то этот код может быть 2-удлинен до линейного кода с блоковой длиной N = п -\- i. Соответствующий 2-удлиненный код строится путем добавления единичного вектора длины N к порождающей матрице кода. Как видно из рис. 14.1, этот код получается из расширенного циклического кода с порождающим многочленом g {х)1(х -Ь 1) путем 1-удли-пепия с помощью общей проверки на четность. В большинстве случаев минимальный вес 2-удлиненного кода совпадает с минимальным весом исходного кода. Однако в некоторых случаях 2-удлинение кода приводит к уменьшению минимального расстояния. Хотя нетрудно найти модифицированную границу Гилберта, из которой следует, что любой достаточно длинный код с малым объемом и средней скоростью может быть 2-удлинен до лучшего кода, метод 2-удлинения оказывается безрезультатным в нетривиальных случаях алгебраической теории кодов. 14.6. 2-укорочение кода (вычеркивание информационных символов) Любой код можно 2-укоротить с помощью вычеркивания информационных символов, причем минимальное расстояние 2-укорочен-пого кода будет не больше минимального расстояния исходного кода, если не позаботиться о специальном выборе вычеркиваемых символов. С теоретической точки зрения мало что известно о целесообразном выбрасывании позиций. Практически циклические коды, как правило, 2-укорачиваются путем вычеркивания последователь-лых позиций, так как этоупрощает их реализацию. 14.7. Подкоды над подполчми 14.71. Определение. Если Л - код длины п над GF (р), где р - степень простого числа ), то подкод кода Ji, состоящий из слов, все координаты которых лежат в GF (р), называется подкодом кода Л над подполем GF (р). Особый интерес представляет случай р = 2. Свойства. 14.72. Подкод линейного кода над подполем линеен. 14.73. Если код А инвариантен относительно некоторой группы. \ подстановок, то любой подкод над подполем также инвариантен относительно этой группы. 14.74. Пусть А - циклический код длины п над GF (р) с порождающим многочленом (14.741) g{x)= П {х-а\ где а - примитивный корень п-й степени из единицы, а К - жко- жество вычетов по mod п. Тогда подкод кода Л над GF (р) является циклическим кодом с порождающим многочленом (14.742) g{x)= П {х-а\ где к К тогда и только тогда, когда кр К для некоторого целого i.l Доказательства. Пусть - множество всех и-мерных векторов над GF (р). Тогда подкод кода над подполем GF (р) определяется равенством = .з П 14.72. U, и ± , U, v6==>u±v6, Следовательно, S = Л [\ - линейный код. 14.73. Пусть я (и)-такая перестановка координат, что хаЛ =Фя(и).. Так как я -перестановка, то и 6 л; (и) 6 , так что] и6=я(и)е.. 14.74. Если .3 - линейный циклический код, то, применяя 1 циклическую перестановку и учитывая свойства 14.72 и 14.73, полу-j чим, что - линейный циклический код. Пусть порождающие мно- гочлены кодов Л и заданы в виде (14.741) и (14.742). Покажем, что 1= и Так как то is: д= 1. Так как д= , то рК = К, так что pK S К[р,ля всех i и (14.743) Для того чтобы показать, что К=[}рК, рассмотрим многочлен i i=0 c{z)= П (з:-а"). Так как [jPKsK, то с{х)с4; так как р {[]рК}= {[}рК}, г i г ТО с{х). Следовательно, с (ж) gfl = Так как каждый корень многочлена g (х) есть корень с(х), то (14.744) кя\}рК. Из (14.743) и (14.744) вытекает, что Z= \}рК. . Если через К ж К обозначить соответственно дополнения К ж К (т. е. K[jK=K[jK = {0,l,2, ...,п-1} и КОК = К[]К=0, то К= (]рК. Иными словами, а -корень проверочного многочлена подкода кода над подполем GF (р) тогда и только тогда, когда а**, а*, аР, . . ., aP*" - множество всех корней проверочного многочлена кода Один частный класс подкодов над подполями будет рассмотрен более подробно в разд. 15.5. 14.8. Прямое произведение кодов и его свойства 14.81. Прямое произведение кодов ). В большинстве случаев координаты кодового слова длины п удобно записывать в виде С = [Со, Ci, Cg, . . ., Cj, • . Cn-i] ). Однако, если n = niX -составное число, то иногда удобнее записывать кодовое слово С в виде X И2)-мерной матрицы 0, Т12-1 1, П2-1
Если символы этого кодового слова должны передаваться последовательно, то одномерная природа времени заставляет нас перевести эту двумерную матрицу в одномерную строку. Для отождествления Ci,j с Ci надо определить i и / как функции от I. Это можно сделать различными способами. Каноническое упорядочение получается при выборе в качестве i и / частного и остатка от деления I на Wj. Это ) Некоторые авторы используют название кронекероеское произведение. ) Везде в разд. 14.8 во избежание путаницы с двумерной записью мы будем использовать знак для обозначения одномерных кодовых слов и их координат. упорядочение имеет вид
... C„j, i • • • С2„2-1 • Сп~1 J Циклическое упорядочение, рассмотренное Бартоном и Велдоном [1965], определяется условиями (48.811) Z = jmodni, Z = /modn2. Например, если = 3 и = 7, то Со Ci5 Cg Сз Cl8 Ci2 CeT С; Cj Cj6 Clo C4 Cj9 Ci3 ~Cj4 Cg C2 Cl7 Сц C5 C20- Если Hi и Aig взаимно просты, то, согласно китайской теореме об остатках 2.16, при OZ<;re циклическое упорядочение устанавливает взаимно однозначное соответствие между числами Z(0-<;Z*<;re) и парами (г, /), где О i Для не взаимно простых щ ж пЛ циклическое упорядочение не имеет смысла. Среди двумерных кодов наиболее интенсивно изучалось введен-! ное Элайесом [1954] прямое произведение кодов. 14.812. Определение. Пусть Jh - линейный код с длиной] Пу, а - линейный код с длинойп. Прямое произведение кодов Л,\ 38 обозначается через А У. и представляет собой {{двумерный» код, \ состоящий из всех кодовых слов длины пп, удовлетворяющих следую-] щим условиям: 1) [Co,j, Ci,j, C,j, . . ., Cni-i,]] J: для всех j; 2) [Ci.o, C;,i, Ci,2, . . ., Ci,„2 i] для всех i. He представляет труда проверить следующие два свойства пря- мого произведения, кодов ): , , (14.813) dim(.;x J)==(dim.)(dim J*). (14.814) (минимальное расстояние {JtxSS)} \ = {минимальное расстояние с} • {минимальное расстояние \ Наиболее естественным способом декодирования канонически! упорядоченного прямого произведения является представленное на рис. 14.2 каскадное декодирование. На первом этапе каскадного декодера используется декодер для кода а на втором - декодер-для кода Л, в котором каждый элемент единичной задержки заменен .1инией, состоящей из п элементов единичной задержки. Последнее позволяет декодировать все Wg столбцов синфазно. Все элементы, появляющиеся на выходе второго декодера в фиксированный момент времени, принадлежат одному и тому же столбцу кода. На первом этапе декодируется каждая строка кода; а на втором этапе - каждый столбец кода. Если даже среди поступающих на первый декодер символов содержится много искаженных, то от первого декодера ко второму (к счастью) передается уже значительно меньше ошибок, а информация, поступающая на выход декодера, по существу вообще не содержит ошибок. Эта простая процедура декодирования в каналах без памяти оставляет желать лучшего. Она приводит к отказу от декодирования при многих ошибках, которые код может исправлять Если 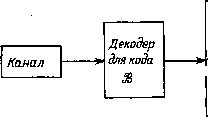 декодер для кода Я,в котором злемент единичной ржкизаменён тлинию из П2 зпеиентов еШтч-ной задержки Получатель данных ) Здесь dim обозначает размерность. Размерность кода равна числу его информационных символов. Ри с. 14.2. Каскадный декодер для прямого произведения кодов, передаваемого в каноническом виде. составляющие коды имеют нечетные минимальные расстояния и то имеются векторы шума веса (di+1) {d--i)/, которые данной процедурой декодируются неверно, хотя код может исправлять все ошибки веса (did - 1)/2 и меньше. Однако процедура каскадного декодирования прямого произведения кодов дает эффективный метод построения реализуемых систем связи для каналов с группирующимися ошибками, так как такие искажения не могут поражать слишком много строк кода. Если прямое произведение передается в циклическом порядке, то пакеты ошибок будут поражать и строки и столбцы. В силу этого обстоятельства циклическое упорядочение часто бывает предпочтительней канонического. Другое интересное свойство циклического упорядочения описывается в разд. 14.82. 14.82. Циклическое произведение кодов. В общем случае прямое произведение двух циклических кодов не является циклическим кодом. Но если блоковые длины исходных кодов взаимно просты, а символы прямого произведения упорядочены согласно правилам (14.811), то такое произведение будет циклическим. Это составляет содержание теоремы 14.821. [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [ 56 ] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] 0.0093 |