но малую вероятность ошибки для всех скоростей, лежащих ниже пропускной способности, несмотря на то, что Шеннон [1956] показал, что бесшумная мгновенная обратная связь не увеличивает пропускной способности любого прямого дискретного канала без памяти.

Лучшие известные асимптотические границы для е (R) - границы Гилберта и Элайеса - применимы к линейным и к нелинейным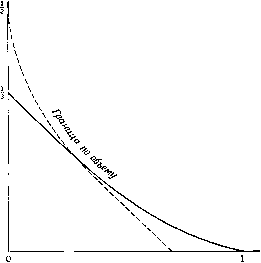

0,2965 0,694

Скорость

Рис. 13.6. Асимптотика корректирующей способности для двоичного сим-1 метричного канала с обратной связью (сплошная линия).

кодам. Предполагается, что нелинейные коды асимптотически не лучше линейных кодов, однако до сих пор это не доказано. Для! некоторых конечных случаев Грин [1966], Джулин [1965], Нейдлер (1962 а, Ь], Нордстром и Робинсон [1967] построили нелинейные! коды, которые лучше любых линейных. Особый интерес представляет; нелинейный «квадратичный» код Нордстрома над GF (2) с блоковой длиной 15, восемью информационными символами Хо, Xj, . . ., X7I и семью проверочными символами Fo, У, . . ., Y. Первый провероч- ный символ Уо определяется соотношением

(13.83) Уо = Хо + Xi + Хз + Хе + Х7 + (Хо -I- X4)(Xi + +Х2 + Хз + Х5) + (Xi + Х2) (Хз + Х5). .

Остальные координаты вычисляются путем подстановки в (13.83) , Xi+j (mod 7, вместо Xi.

Препарата [1968] и Редди [1968] показали, что кодовое расстояние этого кода равно 5. Особый интерес этот код представляет потому, что Джонсон [1962] показал, что ни один двоичный код с ге = 15 и d = 5 не может иметь более чем 2* кодовых слов, а Вагнер [1965] показал, что лучший линейный код с ге = 15 и d = 5 содержит только 2 кодовых слов. Некоторые соображения подсказывают, что соотношения типа (13.83) позволяют строить другие хорошие нелинейные коды, однако никакие конструкции общего типа до сих пор пока не найдены.

Большое число работ посвящено определению функции w (ге, к) - максимального минимального веса для множества произвольных линейных двоичных кодов с блоковой длиной ге и скоростью R = kin. Для некоторых малых значений пик предложено много способов вычисления w (ге, к). Нижняя граница для w (п, к) может быть получена либо путем подбора специальных хороших кодов, либо с помощью модификации Варшамова [1957] или Сакса [1958] для границы Гилберта. Верхняя граница для w (ге, к) исследовалась с помощью большого числа разнообразных методов. Для малых ге - к граница сферической упаковки и ее «квазисовершенный вариант» дают точные результаты. Для малых А; Мак-Дональд [1960] и Грисмер [1960] получили точные границы с помощью модификации рассуждений Плоткина [1960]. Соломон и Стиффлер [1965] предложили класс кодов с малыми скоростями, достигающих границы Грайсмера. Краткое описание кодов Соломона - Стиффлера дается в § 14.2.

Для многих пик точная верхняя граница для w {п, к) получена с помощью методики Джонсона [1962, 1963]. В ряде случаев оказалась полезной граница Вакса [1959]. Некоторые результаты о возможных локальных изменениях w (ге, к) при малых изменениях . и и А; были получены Калаби и Мирваанесом [1964]. Они также построили таблицу известных значений w (ге, к). Некоторые элементы в этой таблице были найдены Вагнером [1965].

Представляется правдоподобным, что вместе с появлением новых быстродействующих вычислительных устройств будут продолжаться попытки отыскания функции w (ге, к) для других пар п ж к. Но пока функция е (R) остается неизвестной, мало что можно сказать о W (ге, к) при больших значениях пик.

гг-658

Глава 14

Коды, полученные путем модификации и сочетания других кодов

Во многих прикладных вопросах возникают специфические допол- . пительные ограничения на коды. Например, может оказаться, что блоковая длина п или число информационных символов к должны; иметь некоторые частные значения, отличные от тех, которые получены при построении кода. Хотя с точки зрения кодовика-теоретика ограничения подобного рода представляются излишне жесткими и нелогичными, не всегда удается от них избавиться. Эти ограничения могут быть учтены в некоторых других частях системы связи, но иногда легче изменить модель кода, чем переконструировать другие блоки системы.

На рис. 14.1 представлены шесть основных способов модификации кодов. Добавляя проверочные или информационные символы, можно увеличить блоковую длину кода, а опуская информационные! или проверочные символы, можно ее уменьшить; можно также при фиксированной блоковой длине увеличивать или уменьшать число слов кода. Для этих шести fосновных типов преобразований кода! мы будем соответственно использовать термины: 1-удлинение, 2-удли- нение, 1-укорочение, 2-укорочение, расширение, сужение ). Эти преобразования кодов 1описаны в литературе, но, к сожалению,! использование соответствующих терминов не во всех работах оди- наково. Так, Казами, Лин и Питерсон используют термин «модифика- ция» там, где Соломон и Стиффлер используют термин «1-укороче- ние». Мы предпочитаем использовать термин «модификация» в качест- ве общего для всех шести преобразований.

14.1. 1-удлинение кода (добавление проверочных символов)

Любой код может быть удлинен путем добавления проверочных* символов, причем минимальный вес удлиненного коданеУувеличит-ся, если не позаботиться о хорошем выборе дополнительных провероч- ,1" ных символов. Добавление общей проверки на четность - наиболее ,-1 распространенный метод 1-удлинения кода, переводящий исходный ».

л = 7, Л = 4 икпичеекий, gix) = + 1

А, = А, = 7

0010111

S<6 = 0101110

1001011

1101000 «в 0110100 "0011010

0001101

Циклический. gU) = (х+1) (х+х + 1)

1111111

0010111 ~ 0101110 1001011

1011100 = 0101110 0010111

2-укорачение

2-удлинение

N=8,k = 4

0 = 8= 1

4= 14

Нециклический

11111111 00010111 00101110 01001011

11111111

о, 01011100 «5 ~ 00101110 00010111

Рис. 14.1. Простейшая иллюстрация к терминам «1-удлинвние, 1-укорочение, 2-удлинение, 2-укорочение, расширение, сужение». Здесь - порождающая матрица кода, т. е. матрица, пространство строк которой образует код. (п - блоковая длина, к - число информационных символов, Ai - число кодовых

слов веса г.)

) Автор использует соответственно терминологию «extend, lengthen, puncture, shorten, augment, expurgate», однако мы предпочитаем избежать буквального перевода этих терминов.- Прим. перев.

КОД С блоковой ДЛИНОЙ И В НОВЫЙ КОД С блоковой ДЛИНОЙ = и + 1 ).

в двоичном случае вес каждого слова такого кода есть четное число. Если исходный линейный двоичный код имел нечетный вес, то при

1-удлинении кодовое расстояние возрастает. Пусть 2 Cjx -слово

i = 0

исходного кода. Тогда остаток от деления этого многочлена на х - 1

равен- Ci, а. 1-удлипение кода равносильно добавлению одного

символа, равного - У\ Ci.

г = 0

В некоторых случаях целесообразно дальнейшее 1-удлинение кода путем добавления дополнительных символов, равных остатку от деления слов исходного кода на некоторый данный многочлен. Например, Андрианов и Сасковец [1966] обнаружили, что двоичный циклический БЧХ-код с блоковой длиной п и конструктивным расстоянием d может быть путем многократного 1-удлинения преобразован в код с блоковой длиной ?г 4- 1-f- deg М"). После передачи исходного кодового слова передается остаток от деления этого слова на х + 1, а затем остаток от деления исходного слова на М-) {х). Такой 1-удлиненный код имеет минимальное расстояние d + 2, так как любая конфигурация ошибок с весом не более, чем {d + 1)/2 может быть исправлена с помощью следующей процедуры.

Сначала декодер пытается декодировать первые ге + 1 символов, , Не обращая внимания на остальные deg М*) символов. Если среди них искажено не более чем {d - 1)/2, то попытка заканчивается успехом и остальные символы (возможно и искаженные) игнорируются. Если среди первых ге + 1 символов искажено точно [d + 1)/2, то начальное декодирование приводит к отказу. Декодер предполагает. Что последние deg М) символов приняты правильно, и по этим символам определяет .S-сумму d-x степеней локаторов ошибок для первых ге + 1 позиций. Используя эту дополнительную информацию, декодер может исправить любые {d -f- 1)/2 ошибок в канале с помощью одного из прямых методов, описанных в гл. 7 и 10.

14.2. 1-укорочение кода (выбрасывание проверочных символов)

Любой код можно 1-укоротить путем выбрасывания проверочных символов, причем минимальный вес 1-укороченного кода будет значительно меньше минимального веса исходного кода, если только не позаботиться о хорошем выборе оставляемых проверочных симво-

) Именно такое 1-удлинение в литературе называется «расширением» (extended) кода.- Прим. nepfe.

лов. в общем случае вес каждого слова исходного кода уменьшается на вес выбрасываемых символов. Следовательно, 1-укорочение линейного кода с минимальным весом d на р позиций приводит к 1-укороченному коду с минимальным весом d - р. Минимальный вес 1-укороченного кода больше d - р тогда и только тогда, когда в исходном коде ни одно из слов веса d не содержит единиц во всех выбрасываемых позициях.

Соломон и Стиффлер [1965[ показали, что при достаточно малых скоростях хорошие линейные коды могут быть получены путем 1-укорочения регистровых кодов максимальной длины. Например, рассмотрим двоичный регистровый код максимальной длины с блоковой длиной 31 и порождающей матрицей

XX Y

Y Y X

Y YY

(14.21) =

0 000100101100111110001101110101 0001001011001I1I100011011101010 0010010110011111000110111010100 0100101100111110001101110101000 ,1 00101100111110001 1 011101010000

Нулевой вектор и 31 столбец этой матрицы образуют 5-мерное векторное пространство над GF (2). Множество из трех столбцов, отмеченных буквой X, и нуль-вектор образуют в нем 2-мерное подпространство, а множество из семи столбцов, отмеченных буквой У, и нуль-вектор - 3-мерное подпространство этого пространства. Каждое слово исходного кода или не содержит ни одной единицы, или имеет две единицы в позициях, отмеченных буквой X, и не имеет ИИ одной, либо имеет четыре единицы в позициях, отмеченных буквой У. Вообще, любое кодовое слово регистрового кода максимальной длины с блоковой длиной 2** - 1 не содержит ни одной единицы, ,(ибо имеет 2~ единиц в 2" позициях, соответствующих ненулевым точкам Z-мерного подпространства. Следовательно, если выбросить из регистрового кода максимальной длины точки, соответствующие .шнейно независимым подпространствам размерностей Zj, 1, .., где

(14.22)

то блоковая длина и минимальное расстояние изменяется в соответствии с формулами

(14.23)

« = 2-1, „=2-l-2(2"-l), d = 2-\ d = 2-i-22~.

[Тапример, если выбросить из матрицы (14.21) позиции, отмеченные оуквами X и У, то получим укороченный код с блоковой длиной 21,