путем решения системы т линейных уравнений с т неизвестны! над полем GF {р).

В частном случае квадратного уравнения над GF (2*") можн избежать перехода к системе линейных двоичных уравнений! С помощью соответствующей замены переменных квадратное урав пение общего вида без кратных корней можно привести к вид

-j- у = и. Линеаризированная часть этого многочлена имеет оди1 и тот же вид для всех квадратных уравнений над заданным нолем! так что решения всех этих уравнений могут быть найдены и фикси- рованы в виде соответствующей матрицы.

Согласно теоремам 6.69 и 6.695, уравнение у у = и имее! решение в GF (2™) тогда и только тогда, когда Тг (и) = 0. IlycTi а - произвольный элемент поля степени т над GF (2), а а** - эле мент, для которого Тг (а) = 1. Тогда для i = О, 1, 2, . можно найти такое г/;, что

(11.14) yl + yi = {,

если Тг(а*) = 0; если Тг(а*) = 1.

Для решения уравнения г/ + г/=и= 2 tt UiGF{2), положи»

г/= S Utyt. Тогда

т-1 m-i

У+У=1] Ui{y! + yt) = ua S C/jTr(a*) =

= a" Tr ( S Uta) = w + a" Tr (u). J

Следовательно, если Тг (и) = О, то два решения квадратного урав-=

m-i m-i

нения у + у = и имеют вид г/= У\ Utyt и г/= 1 + 2 iVi-

i=0 i=0

11.15. Пример. Рассмотрим квадратные уравнения над, GF (2). Если а - корень многочлена а; + + 1, то Тг (а) = = Тг (а) = Тг (а*) = 0, а Тг (1) = Тг (а) = 1. Полагая а" = 1, легко проверить, что решениями уравнения (11.14) являются

У1 = а

У2 = у1=-а + а г/з = аЧ-а*

= 00000, = 00010, = 01010, = 00101,

Решения уравнения у + у - и могут быть найдены с помощью схемы, изображенной на рис. 11.1. Если в ячейке Тг (и) появляется 1, то квадратное уравнение г/ + г/ = м не имеет решений. Если в ячейке Тг (и) появляется О, то два решения квадратного уравнения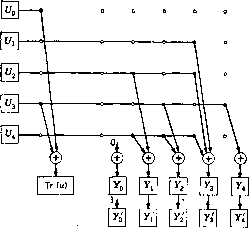

= г/ = а + а2+ «3 = 01110.

Рис. H.li Схема для решения уравнения г/ + у = и в поле GF (2)

у + у = и возникают в регистре г/ и в регистре у. Например, если и = 01001, то в ячейке Тг (и) появится О ж у = 01100=«9, г/ = 11100 = а".

11.2. Наименьшее аффинное кратное

К сожалению, над полем GF (р™) мало аффинных многочленов. Над полем характеристики 2 квадратные многочлены - аффинные, а кубические - нет. Однако если умножить кубический многочлен па соответствующий линейный множитель, то получается аффинный многочлен четвертой степени. Корни кубического многочлена могут быть теперь легко найдены среди корней аффинного многочлена четвертой степени.

В общем случае если / (z) - произвольный многочлер степени d, то алгоритм 11.21 позволяет найти аффинный многочлен, кратный / (з).

11.21. Алгоритм. Для определения аффинного многочлена L (z) - и, кратного многочлену / (z) степени d над GF (р"), следует

= 0.

Эта система d уравнений относительно d + 1 неизвестных всегда имеет но крайней мере одно ненулевое решение, которое может быт найдено с помощью методов, описанных в разд. 2.5. Если [и, Ll, . . ., Ld~i\ - решение этой системы, то А [z) = L {z) - и -аффинное кратное / (z). Если на шаге 11.213 имеется несколько реше НИИ, то среди них можно выбрать нормированный многочлен А (г наименьшей степени. Такой многочлен А (z) называется наижньшь аффинным кратным многочлена / (z).

11.22. Пример. Пусть

/ (z) = z6 + aV + a"z3 + az + a"z + a,

где a* + + 1 = 0 над GF (2*). По модулю / (z) имеем

Z = «2224 „1823 4 „1922 „16z + „13

26 „2225 „1824 „гЗ „1622 XZ - = («18 + «13) Z* + («19 -t- «9) Z3 + («" + «1») Z2 -f-

+ («i3 + «)z+«* = = «IV + aiz 4- az2 -f- a3z + «*,

27 = „2824 „122З 0z2 4 «iez + «2»,

z2 = z8 = «зг* 4- «"z3 + «V 4- «"2 4 «1», z2* = 2" = «z8 + «звг" 4 «12* + «i2z2 + «2» =

s «22* +«28z3 + «5z2 + ««Z + «15,

1) Для большого p класс вычетов для zV легко вычислять путем умножен!

соответствующих из классов вычетов г, z, z, z, . . ., z2 . Для / = 1, 2, . . ., d-1 класс вычетов r<i) (z) находится затем из сравнения гО) (z) = zPr(i-i) (2).

[С/, Lq, Z-2, l3, l4]

0 0 0 0 1

0 0 0 1 0

0 0 10 0

1 0 0 0 0

«15«« «««ie

= 0.

Это дает решение [«*, a", «1®, «

„29 „28 „5 „6 „15j

«13, 1], так что U = a\ L (z) =

= a2<*z + «i8z2 4- aV 4 «1 4- zi*. Для определения корней этого аффинного многочлена в GF (2*) находим

L (1) = а» + «13 + «3» + «18 + «20 = о,

L (а) = «18 + «21 + «3 + «20 + «21 = 1 4- а + «2 + «3 + «*, L («2) = «1 + «29 + а 4- а + «22 = i + „ + «2 + «з -f «*, L («3) = «17 4- «« + «11 + «2* + «23 = 1 + а + «2 + а\ L («*) = «2 + «1* 4- «15 4- «2 + «2* = 1 4- а 4- «2 + «3,

так что X имеет следующий вид

"0 0 0 0 0 11111 = 11111 11110 11110

Решениями уравнения ZX = [О, О, О, О, 1], очевидно, являются 00101, 00110, 01001, 01010, 10101, 10110, 11001, 11010 (log„ 2 = 6, 7, 8, 17, 20, 22, 27, 30). Среди этих 8 корней многочлена А (z) имеются U все корни многочлена / (2) в GF (2*). Оказывается, рассматриваемый многочлен / (z) имеет в GF (2) корни а, « и а".

* 11.3. Общие свойства линеаризированных и аффинных многочленов

В этом разделе мы докажем общие свойства аффинных многочленов. В последующих разделах настоящей главы будут даны приложения этих результатов к некоторым вопросам теории кодирования. Основные идеи всех результатов данного раздела принадлежат Оре 11933, 1934], хотя многие из этих теорем были недавно независимо передоказаны несколькими специалистами по теории кодирования.

11.31. Теорема. Многочлен L (z) является линеаризированным тогда и только тогда, когда его корни образуют линейное пространство над GF (р) и все имеют одну и ту же кратность, равную степени числа р.

11.211 1). Вычислить £ mod / (z) для к - d, d + 1, . . ., ...Ad-i)p.

11.212. Используя результаты предыдущего шага, определит! (z), r(i) (z), . . ., rC-i) (z), где zP sH) (z) mod / (z).

11.213. Решить систему линейных уравнений

р-1 р-1 р-1 п ь

b{z) = [ П П ••• П (z-S.n)r.

С1=»0 i=l

Положим

п=0 "«-1=0

/<« (z) = z,

С1=0

/<2) (z) = П (Z - ciri - С2Г2) = П (Z - СгГа)],

С2=0 С1=0 С2==0

р-1 р-1 Р-1 г+1

i+i=<i=o с1=о 3=1

= П r(z-Ci+in+i).

=i+l=0

Ясно, что L(z) = [/(">(z)]p h.

Общие свойства линеаризированных и аффинных многочленов 257

Докажем теперь индукцией по i, что (z)-линеаризированный многочлен. Это утверждение очевидно для i = 0. Пусть (z) - линеаризированный многочлен. Тогда

Г> (Z - Ci+in+i) = /< (Z) - С;+,/<Ь {Гi+i)

= [/b(z)f-/<* (Z) (гж)]-

Так как /О (z) -линеаризированный многочлен, то его скалярное кратное ЯЧ) [/<4j+i)]~ и его р-я степень [/() (z)] - также линеаризированные многочлены. Разность двух линеаризированных многочленов является линеаризированным многочленом, поэтому /{+!) (z) линеаризирован. Следовательно, /(") (z) - линеаризирован-иый многочлен и потому линеаризирована и его р-я степень L (z). щ

Аналогичный результат для аффинных многочленов содержится в следуюш;ей теореме:

11.32. Теорема. Многочлен А (z) является аффинным тогда и только тогда, когда его корни образуют аффинное пространство над GF (р) [т. е. если s, s, . . ., Sn ~ его корни, то и -\-+ (fe ~ i) ~ также его корень для любых с g GF (р)] и все имеют одну и ту же кратность, равную степени числа р.

Доказательство. Пусть А {z) = L {z) - и - аффинный многочлен. Если s, s, . . ., - корни А (z), то L (s) = ияз - - - корень L (z) для каждого А; = 1, 2, . . ., п. Следовательно,

L (si + 2 Cfe (Sft - si)) = L {si) = li И, значит, Sj + 2 {su - - корень многочлена A (z). Это означает, что корни аффинного многочлена образуют аффинное пространство.

Производная аффинного многочлена А (z) = L (z) - и равна коэффициенту Z/Q npnz. Если ЬфО, то все корни А (z) различны. Если же Lo = Z/1 = . . . = Ь 1 = О и Lf Ф О, то А (z) есть р-я степень аффинного многочлена с различными корнями, и, следовательно, каждый корень А (z) имеет кратность р*.

С другой стороны, если корни некоторого многочлена образуют аффинное пространство, то разности этих корней образуют линейное пространство. Согласно теореме 11.31, многочлен, корнями которого служат различные элементы этого линейного пространства, есть линеаризированный многочлен L (z). Если s - произвольный корень А (z), то L (s - Si) = О, или L (s) - и = О, где и = L (s). Следовательно, корни А (z) суть корни многочлена L (z) - и, и так как

Замечание. Корни многочлена L (z) не обязательно лежат в GF {рУ, они могут лежать в некотором расширении этого ноля!

Доказательство. Необходимость. Пусть L (z) - линeaj ризированный многочлен, г, г, ... - его корни, а с, . . 6 eGF{p). Тогда L{crk) = i]ckL{rk) = О и, следовательно,! ЗЛ - также корень L (z). Значит, корни L (z) образуют линей- ное пространство над GF (р). [

Производная многочлена I/ (z) = L;zp равна Lq. Если Ь„ Ф 0J

то L (z) не имеет кратных корней. С другой стороны, если = = . . . = = О, но Lft ф О, то

L(z) = SL;z = (SLp-V-y

i - г

является p-й степенью линеаризированного многочлена без крат ных корней. В этом случае кратность каждого корня многочлену L (z) равна р*".

Заметим, что если Li 6 GF (рП, то Lf" 6 GF (/)").

Достаточность. Пусть корни многочлена L (z) образуют линей ное пространство над GF (р); выберем в нем базис г, г, Гд, . . . , г„ Каждый корень многочлена L (z) может быть однозначно записар

в виде Z = 2 ii для некоторого подходящ,его набора коэффициен!

1=1 f

тов Cj. Не ограничивая обш,ности рассуждений, можно считать много!

член L (z) нормированным. Тогда