Глава 8 Недвоичное кодирование

8.1. Схемы модуляции

До сих пор мы рассматривали только задачу кодирования и декодирования для двоичного симметричного канала, входные и выходные символы которого суть О и 1.

В большинстве приложений кодовая последовательность из нулей и единиц подается на модулятор, превращаюп],ий эти символы в определенные функции времени. Результирующие временные сигналы

Рис. 8.1. Представление символа 0.

Рис. 8.2. Представление символа 1.

используются для управления амплитудой передаваемых сигналов, которые могут представлять собой, например, напряжение или мгновенную мощность, излучаемую радиопередатчиком.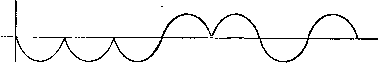

Рис. 8.3. Представление последовательности 0001101.

Например, символу О может соответствовать функция, изображен-: пая на рис. 8.1, а символу 1 - функция, изображенная на рис. 8.2. При этом кодовой последовательности 0001101 будет соответствовать модулирующая функция, изображенная на рис. 8.3. Аддитивный шум приводит к тому, что на приемное устройство поступит сигнал, изображенный на рис. 8.4. Предположим, что приемное устройство осуществляет квантование полученного непрерывного сигнала на соответствуюпще временные интервалы, как показано на рис. 8.5. Каждый отрезок функции на этих интервалах демодулируется затем!

с наибольшей вероятностью как О или 1. Полученный сигнал, изображенный на рис. 8.5, должен быть демодулирован как 0001001. Демодулированный сигнал подается на декодер, который должен попытаться исправить ошибку в пятой позиции.

Хотя символы О и 1 можно представлять многими различными спо- , собами, каждый конкретный выбор сигналов не существен для

Рис. 8.4. Наложение шума на последовательность 0001101.

устройств кодирования и декодирования. Они оперируют только последовательностями из нулей и единиц, которые кодер посылает на модулятор, а декодер получает с демодулятора.

В недвоичном случае также возможны многие схемы модуляции. Мы кратко рассмотрим три таких способа для алфавита из пяти символов: О, 1, 2, 3, 4. Они изображены на рис. 8.6.

Р и с. 8.5. Квантование на временные интервалы зашумленного представления последовательности 0001101.

При использовании ортогональной модуляции кодовое слово 140343 представляется сигналом, изображенным на рис. 8.7. При прохождении по каналу передаваемый сигнал искажается шумом. Полученный сигнал может иметь вид, представленный на рис. 8.8. Приемник демодулирует сигнал и перекодирует его в последовательность символов. Если шум в канале слаб, то демодулятор сравнительно легко принимает правильные решения. В рассматриваемом примере демодулятор сможет правильно демодулировать первый символ как 1 и второй символ как 4. Может, однако, возникнуть и более сильный шум, приводящий к ошибке демодуляции. В данном примере демодулятор может решить, что третий символ есть 1. Такое неправильное решение называется ошибкой в символе. Так как в течение четвертого временного интервала шум слаб, то демодулятор правильно решает, что четвертый символ - 3.

На пятом временном интервале сигнал настолько слаб, что демодулятору лучше ничего не делать, чем принимать сомнительное решение. Демодулятор отказывается от выбора из одинаково плохих возможностей и называет соответствующую букву стертой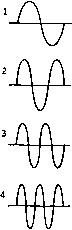

Орпюгональная Амплитудная Фазовая модуляция модуляция модуляция

Рис. 8.6. Три вида модуляции для алфавита из пяти символов.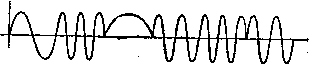

Рис. 8.7. Представление последовательности 140343 сигналами ортогональной

модуляции.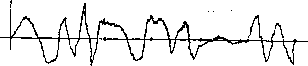

Рис. 8.

Наложение шума на ортогонально модулированный Вигнал, преД" ставляющий последовательность 140343.

(мы ее обозначим через ?). В одних случаях мы будем допускать стирание, а в других нет. Если стирания не допускаются, то навяжем демодулятору решение 0. Последний символ в любом случае демоду-лируется правильно, так что принятая последовательность символов будет иметь вид 1413?3 или 141303, в зависимости от того, допустимы пли нет стирания.

Для построения линейных кодов для недвоичных каналов в множестве входных символов полезно ввести арифметическую структуру. Если число q символов входного алфавита есть степень простого числа р, то в качестве такой структуры может быть взята арифметика поля GF (д). Как и в двоичном случае, переданные и полученные последовательности можно рассматривать как векторы над этим полем. Разность между полученной и переданной последовательностями есть вектор шума. В предыдуп],ем примере переданная последовательность над GF (5) имеет вид 140343, а принятая последовательность - 1413РЗ или 141303, и разность этих векторов равна 0010Р0 или 001010. Как и в двоичном случае, линейный код может быть определен как множество векторов, транспонированные к которым лежат в нуль-пространстве проверочной матрицы S£- Полученное слово R имеет синдром S = cR, равный синдрому вектора ошибок, т. е. = S£E. Множество кодовых слов образует аддитивную группу; множество полученных слов с одним и тем же синдромом образует (Смежный класс по этой подгруппе. Для фиксированного-полученного слова множество возможных векторов ошибок образует смежный класс, содержащий это слово. Задача декодера может быть, таким образом, сформулирована так: по заданному синдрому полученного слова найти наиболее вероятный вектор шума, лежащий в смежном классе слов с этим синдромом.

8.2. Весовые функции

Как должен декодер выбирать наиболее вероятный из векторов ошибок с одним и тем же синдромом? В двоичном случае ответ сводится к выбору слова с минимальным весом, где вес слова определяется как число единиц среди его п координат. В недвоичном слу-lae, так же как и в двоичном, можно в качестве лидера смежного класса выбрать слово с минимальным весом. Однако в зависимости от используемой схемы модуляции вес слова можно определять многими различными способами. Мы рассмотрим два определения, принадлежащие Хэммингу [1950] и Ли [1958].

8.21. Определение. Весом Хэмминга слова Со, Ci, Cj, . . . • . ., Cn-i, Ci £ GF (q) называется сумма весов Wh Хэмминга его координат, где

гн(Сг) =

о, если Ci = О, если Сг=/=0.

8.22. Определение. Весом Ли слова (7q, с2, • • п-i, Ci 6 GF (р) называется сумма весов Ли его координат, где

Wl (Ci) = I I, \Ci\ = ±Cimodp, 0 < I I < pl2.

Bee Хэмминга и вес Ли могут быть определены и для тех алфавитов из q букв, в которых q не является степенью простого тасла. Однако при выходе за пределы конечных полей появляются определенные трудности в построении циклических (и вводимых ниже негацикличе-ских) кодов. Для избежания этих трудностей мы будем рассматривать только алфавиты из q = букв, где р простое.

В случае метрики Ли мы будем предполагать, что q = р простое, так как вычеты по модулю q образуют поле тогда и только тогда, когда q простое.

Системы с ортогональной модуляцией хорошо описываются метрикой Хэмминга. В частности, можно показать, что если буквы алфавита модулируются в виде ортогональных сигналов, на которые в канале накладывается аддитивный белый гауссов шум, то все ошибочные переходы символов друг в друга равновероятны. Следовательно, вероятность вектора ошибок зависит только от числа его ненулевых координат и не зависит от конкретного значения этих ненулевых координат. Метрика Хэмминга хорошо позволяет выделить более вероятные ошибки, предполагая вероятными ошибки малого веса, а ошибки с большим весом - маловероятными.

Метрика Ли хорошо соответствует схемам с фазовой модуляцией. Если на фазо-кодированные сигналы накладывается аддитивный гауссов шум, то намного более вероятно, что шум переведет переданную букву в букву, близкую по фазе, чем в букву с сильно отличающейся фазой. Значения ±2 ненулевых координат в векторе ошибок значительно менее вероятны, чем значения ±1. Метрика Ли дает хорошее приближение к реальной ситуации; в общем случае она предполагает ошибки малого веса более вероятными.

В случае каналов с амплитудной модуляцией и аддитивным гауссовым шумом и метрика Хэмминга и метрика Ли обладают некоторыми очевидными недостатками. Вероятность перепутать наибольшую и наименьшую амплитуды значительно меньше, чем вероятность перепутать две соседние амплитуды, расположенные около середины алфавита. Однако, если число символов в алфавите велико, то метрика Ли дает приемлемое приближение. Описание с помощью метрики Хэмминга является более грубым.

Для некоторых каналов оказываются полезными совсем другие определения весовых функций. Однако мы сосредототам наше внимание на метрике Хэмминга и метрике Ли.

При построении систем модуляции и демодуляции приходится рассматривать многие вопросы. Необходимо выбрать множество сигналов и правило демодуляции. В общем случае этот выбор суще- \ ственно зависит от конкретных характеристик канала связи. При этом

приходится учитывать мощность шума, спектр шума, частотные ограничения на передатчик, ограничения на мощность передатчика и возможность межсимвольной интерференции. Этим задачам посвящено большое количество работ, но мы на них останавливаться не будем. Заинтересованный читатель может обратиться к книгам Давенпорта и Рута [1958] или книге Возенкрафта и Джекобса [1965]. Для понимания последующих глав этой книги абсолютно необходимым является лишь общее знакомство с этой областью. Мы полагаем, что модулятор, демодулятор и весовая функция (Хэмминга или Ли), заданы, и концентрируем свое внимание на задаче исправления ошибок (или ошибок и стираний) демодулятора с помощью подходящих способов кодирования и декодирования).

Задача

8.1 (Коды Грея 2)). Некоторые системы связи работают следующим образом: сначала блок из Л га символов р-ичного источника кодируется кодовым словом С = [Со, С), . . ., C„ i] «хорошего» кода со скоростью R и длиной п над GF (р). После этого га позиций этого кодового слова разбиваются на ra/s последовательных подблоков, С = [х<°), х1>, . . ., х"°""М, где каждый подблок х есть последовательность из S элементов поля GF (р): к = [хд, Xi, . . ., Xg.,]. Затем для каждого i вектор х<*> модулируется в одноуровневый сигнал = / (х<)), где / (х) - числовая функция, принимающая значения лишь в промежутке О

< / < р« - 1. Сигналы г/<°), у<-У, . . ., г/("-1) передаются по каналу с белым шумом. Полученные сигналы демодулируются как zC), z<-\ . . ., 2*"*") и преобразуются в s-позиционную р-ичную последовательность v"), v<i>, . . ., v"*~\ где z<<) = / (vt")- Полученный таким образом вектор R = [v", v<i>, . . . . . ., = [Rji, Rj, . . R i] интерпретируется как одно слово над GF (р) длины га и декодируется с помощью алгоритма, согласно которому принимается решение С, если расстояние Ли между С и R достаточно мало.

Рассмотрим два способа задания функции / (х) = 2 ft W Р О < /; (х) <

< р, а именно

(a) fi (х) = Xl для i = О, 1, 2, . . ., S - 1;

(b) fi (х) = Xi - Xi+i mod р для i = О, 1, . . ., s - 2, (х) = x.i. Показать, что если используется правило (Ь), то расстояние между х и v

не превосходит z - г/ , а если используется правило (а), то расстояние между X и V равно S, даже когда \ z - у = 1.

) В заключение этой главы хочется подчеркнуть, что выражение «код с исправлением ( ошибок в данной метрике» означает, что код исправляет все векторы ошибок, вес которых < t в той же метрике. Это существенно при переходе к 9-ичным кодам, где, например, в метрике Ли (в отличие от метрики Хэмминга) величина t учитывает не только число искаженных позиций, но и шачения ошибок в каждой позиции.-Прим. перев.

2) В задаче 8.lb х - представление целого числа / в коде Грея.