
 |
|
Главная страница Алгебраическая теория кодирования [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [ 30 ] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] Код, исправляющий одну ошибку, имеет 5 проверочных и 26 информационных позиций и скорость 26/31. Код, исправляющий две ошибки, имеет скорость 21/31. Эти коды мы уже рассматривали в разд. 5.1 и 5.2. Отметим, что БЧХ-код, исправляющий 4 ошибки, совпадает с кодом, исправляющим 5 ошибок, так как минимальные многочлены Af(*) (х) и Af() (х) элементов а* и соответственно совпадают. Аналогично, код, исправляющий 6 ошибок, совпадает с кодом, исправляющим 7 ошибок. Скорость этого кода равна 6/31. Отметим также, что коды, исправляющие от 8 до 14 ошибок, также совпадают между собой и имеют скорость 1/31. Такой код «одержит только два слова - (00 ... 0) и (И .. . 1). Ясно, что этот код, в каждом слове которого информационная позиция повторяется 31 раз, позволяет одновременно исправлять 15 ошибок. Код с повторением легко может быть декодирован с помощью тривиальной мажоритарной логики, описанной в разд. 1.1. Как будет локазано в разд. 15.4, обобщение этого алгоритма может быть лспользовано для декодирования некоторых других низкоскоростных БЧХ-кодов. К сожалению, эта техника оказывается мало пригодной для декодирования БЧХ-кодов со средними или высокими скоростями. Поэтому мы сначала опишем общую алгебраическую лроцедуру декодирования, применимую ко всем двоичным БЧХ-кодам. При декодировании БЧХ-кодов со средними и высокими скоростями эта процедура является наилучшей из всех известных алгоритмов. Она приемлема также для декодирования БЧХ-кодов с низкой скоростью, хотя в некоторых случаях оказывается хуже, чем алгоритмы, описанные в разд. 15.4. 7.2. Ключевое уравнение для декодирования двоичных БЧХ-кодов Если кодер передает слово двоичного БЧХ-кода C{x)=Cix\ а шум в канале задается вектором £ (ж) = 2 Eix\ то полученное слово записывается многочленом R (ж) ="S RiX - "S Cix +"S Eix\ i=0 i = 0 i=0 Для 7 = 1,2, . • •, 2i кодовое слово кратно минимальному многочлену элемента а и, следовательно, R (а) = О -Ь "S Eia = S = S3, i = U f"- з¥1 Определим многочлен со (z) = 2 <»ft2 с помощью равенства ft=0 (7.22) (z)=a(z)+ SZ,z П (l-Xjz). 1=1 Зф1 где элементы ноля Галуа Х, Х, . . ., Хе ~ локаторы ошибок Ei = 1. Как было показано в разд. 5.2, Sj = R (а) = г<-) (а), где г(ж) - остаток от деления R (х) на минимальный многочлен МО (х) элемента а (1 < / < 2t). После вычисления S, S, . . . . . ., Sit основная задача декодера - определить Х, Х, . . ., Xg из уравнений Z--=5,-, / = 1, 2, 2t. В общем случае эта система имеет много решений, каждое из которых соответствует различным векторам ошибок, лежащим в одном классе смежности по аддитивной группе кодовых слов. Декодер должен найти решение с наименьшим возможным числом е. Для решения системы декодер сначала пытается определить коэффициенты многочлена локаторов ошибок (7.21) (см. также уравнение (1.46)). 7.21. Определение a(2)=ri {i-Xiz)=.l+j]ajz\ • »=i }=i Если многочлен а (z) уже найден декодером, то, используя процедуру Ченя, можно найти взаимные корни для а (z). Ошибки после этого могут быть исправлены с помощью схемы, изображенной на рис. 5.14. Наиболее тяжелая часть этой процедуры - определение коэффициентов oj по величинам Sj. Для того чтобы найти зависимость между величинами Oj и Sj, введем производящую функцию j=i 3=1 t=i i=i После умножения на a(z) имеем S (Z) а (Z) = 2 П (1 Z,z) = 2 Z,z П (1 - Xjz). i=l 3=1 i=l 3Vi Прибавив к обеим частям равенства a(z), получим [l + S (z)] а (z) = а (z) + S Zz Д (1 - Xjz). 188 Гл. 7. Двоичные БЧХ-коды, исправляющие многократные ошибки Тогда [1 + 5 (2)] а (z) = (о (z). В общем случае декодеру известны коэффициенты только при первых 2t степенях z в .S" (z) и не известны коэффициенты St+i «г+з» 524+3, .... Иными словами, декодер не знает S (z), но знает S (z) mod z+. Поэтому естественно ввести уравнение, которое мы назовем ключевым: (7.23) [1 + 5 (z)] а (z) = со (z) mod z+i. Из этого уравнения по заданному S (z) нужно найти оба многочлена а (г) и (о (z), степени которых не превосходят е, где е - число ошибок в канале. Одна «физическая интерпретация» ключевого уравнения была предложена Месси [1968]. Перепишем уравнение в виде -5(1+ S 0Sft-i + (Tft = Wftf или в виде ft-i 5fc=cuft- S OiSh-i - Ok Последнее равенство задает к-ж выход регистров сдвига, приведенных на рис. 7.1 и 7.2, обратные связи которых соответствуют многочлену а {£), а начальное состояние ячеек - многочлену со (г). Это 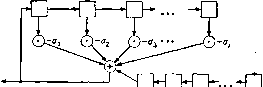 Выход Итальнае-Г „ состояние »2 Рис. 7.1. Интерпретация ключевого уравнения с помощью регистра сдвига с обратной связью. позволяет интерпретировать ключевое уравнение как математическую постановку задачи синтеза регистра с обратной связью: по заданной выходной последовательности 1 + 5 (z) необходимо определить обратные связи 0 (z) и начальное состояние со (z) кратчайшего (наименьшего) регистра сдвига с выходной последовательностью 1 + 5 (z). В задаче декодирования двоичных БЧХ-кодов реальный интерес представляет только многочлен о (z), а не многочлен со (z). Однако это же ключевое уравнение возникает и в некоторых других приложениях. Мы вернемся к нему в гл. 9 и 10, где оно интерпретирует- Начальное аютояние Выход Д 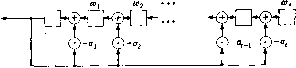 Рис. 7.2. Другая интерпретация ключевого уравнения с помощью регистра сдвига с обратной связью. ся как задача синтеза регистров с обратной связью, и оба неизвестных многочлена 0 (z) и а» (z) представляют непосредственный интерес. Рассмотрим теперь алгоритм решения ключевого уравнения над произвольным полем. 7.3. Эвристическое решение ключевого уравнения Нам надо решить ключевое уравнение (7.23) (l + 5)0 = o)modz2+i относительно многочленов 0 (z) и © (z) при заданном многочлене S (г) mod z+. Разобьем эту тяжелую задачу на ряд этапов. Рассмотрим последовательность уравнений (7.301) (1 + S) о<*> = (о<*> mod z*+i и для каждого А = О, 1, 2, . . ., 2 найдем многочлены, удовлетворяющие этим уравнениям. В общем случае они могут иметь много решений. Так как степень а (z) равна числу ошибок, то хороший декодер должен попытаться найти решение с «малыми» степенями 0 и (В. Если уравнения (7.301) уже решены, то та же пара многочленов <о(*) и о*), вообще говоря, не удовлетворяет сравнению (1 + S) 0W = (о<) mod г+з. (1+5) 0W = аW + z+i mod z+, )фициент при z в произведени] Если Д][ = О, то, очевидно, можно положить ot***) = ot) Однако (7.302) где AJ - коэффициент при 2*+ в произведении (1 + 5) а-К И й)(+) = «>(). Для определения а(+) в случае, когда Д" Ф О, введем вспомогательные многочлены т() и y<), которые определяются как решения вспомогательного уравнения (7.303) (1 +5) тС) = 7"+2" mod 2"+!. При этом, конечно, желательно, чтобы степени многочленов т") и у) были малыми. Определим последовательности {а} и {со} с по-мош;ью вспомогательных многочленов т и у равенствами (7.304) aC+i) =aV)-fzx~), (7.305) (oC+i) = coW - Легко видеть, что многочлены о***) v co(+) удовлетворяют сравнению (1 + 5) aC+i) = coC+i) mod z+D+S если cr() и <»() - решения сравнения (7.302), а т() и у> - решения сравнения (7.303). Суш;ествуют два очевидных способа задания многочленов т") и v*")- Либо (7.306) либо (7.307) ZY), (ft) Если at) и cot) удовлетворяют сравнению (7.302), а т**) и уС**) удовлетворяют (7.303), то многочлены (7.306) и (7.307) удовлетворяют сравнению (1 + 5) tC+i) == vC+i) + z+i mod z+2. Если AW = 0, to выражения (7.307) не определены и нужно использовать формулы (7.306). Если AW Ф О, то выбор между (7.306) и (7.307) должен основываться на минимизации степеней т) и yi-). Степени многочленов о), т**), (й<) и у) задаются следуюш;ими соотношениями: (7.308) degoC+i) degaW, если A*i = 0 или если dega()>degT() + l; 1-1- degtW, если -фО и если deg тС») > deg - 1; dega(+i)< любое из пре-дыдуш;их чисел [ ,если Af=50 и если J dego() = l+degT<); (7.309) degxC+i). (7.310) degco(+i) = \ l + degTW, если выбраны (7.306); [ degаС), если выбраны (7.307); degcoW, если Ai = 0 или если degco()> 1 + degv l+degyC), если AfO и если degv()>degcoW -1; , ,ь4.п / любое из нре- \ .(ft) , л +<\дыдущих чисел ).еслиЛ\=0 и если degoW = 1 +degYW; (7.311) degv(+i) = l + degYC*), если выбраны (7.306); deg&)(), если выбраны (7.307). j(A+l) Степень многочлена ai"") может случайно увеличиться, еслж deg ot) = 1 + deg т() и старшие коэффициенты многочленов а> и А) т() равны. Для того чтобы избежать таких случаев, мы при выборе между (7.306) и (7.307) будем учитывать не степени многочленов а), т(), (о() и у), а некоторую числовую функцию D (к), которую определим следующим образом: (7.312) (7.313) deg оС) < D (к), deg Tt") k-D (к). В силу соотношений (7.308), (7.312) и (7.313) можно дать следующее рекурсивное определение функции d (к): (7.314) D{k+l) = -{ D{k), если Af> = 0 если D{k)>-±; k-\-D{k), если AitO и £)(А;)<У:1, Легко видеть, что если deg о) Z) (А;) и deg т) к - D (к)у то deg а(+1) D (к -\- 1). Аналогично, если deg ©f) < D (к) и deg Y") k-D (к), то deg со+М D (к + 1). Для того чтобы обеспечить неравенства deg т*) (А; + 1) - - £» (А; + 1) и deg y- < (А; + 1) - D (А; + 1), введем следующее правило выбора между (7.306) и (7.307): (7.315) Выбрать (7.306), если о или если D {к) "> (7.307), если АфО и £>(А;)< [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [ 30 ] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] 0.0116 |