жат «буферное» слово; последние п - i ячеек буфера содержит последние (тг - 1)-позиций выводимого слова. Схема Ченя каждый раз вычисляето (а) и определяет, надо или не надо исправлять символ, выводимый из буферного устройства. Регистры сдвига предназначены только для выполнения деления на неприводимые множители

Символы из канала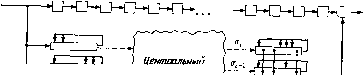

Исправленные символы

+>

Устройетва для деления входного слова на каждый неприводимый делитель порождающего многочлена

7Лок для выполнения операций в пале Галуа (опре деление noSi)

Рис. 5.14. Общий вид декодера для циклического кода.

порождающего многочлена. Центральное устройство обработк! осуществляет построение многочлена локаторов ошибок для буфер-»! ного слова. Когда приняты все п символов входного блока, все символы выходного блока находятся в левой части регистра. Прв

~n-t

Входящие символы

Буферные символы

Выходящие символы

Рис. 5.15. Содержимое буферного устройства в типичный момент времени!

этом содержимое буферного устройства имеет вид, изображенны! на рис. 5.16. После этого буферный блок становится выводимым слс вом, а вводимое слово - буферным блоком. Коэффициенты многс члена локаторов ошибок, вычисленные в центральном устройств обработки, поступают в схему Ченя, а полученные в регистраз остатки от деления принятого слова на неприводимые делител порождающего многочлена - в центральное устройство обработка

В течение времени приема следующих п позиццй вводимого из канала слова центральное устройство обработки должно определять коэффициенты многочлена локаторов ошибок для буферного блока.

Регистры, осуществляющие деление входящего многочлена на неприводимые делители порождающего многочлена, и схема Ченя должны работать синхронно с буфером. Однако центральное устройство обработки, вообще говоря, не связано с остальными частями декодера, за исключением моментов вывода уже вычисленного многочлена локаторов ошибок и ввода синдрома для следующего блока. При этом вывод и ввод центрального оператора не обязательно должны осуществляться одновременно. Если быстродействие центрального устройства обработки столь велико, что оно может вычислить

Р и с. 5.16. Содержимое буферного устройства после окончания приема блока.

многочлен локаторов ошибок до момента ввода нового слова, то объем буферного устройства можно уменьшить. Например, предположим, что центральное устройство обработки может вычислить многочлен локаторов ошибок за половину времени, необходимого для ввода из канала блока из п позиций. В этом случае в буфере должны запоминаться только З/г/2 позиций. К моменту получения всего слова и началу вывода его из буфера центральное устройство обработки вычисляет его многочлен локаторов ошибок. Многочлен локаторов ошибок поступает в схему Ченя, а центральное устройство обработки не используется до тех пор, пока не будет получена остальная часть вводимого слова.

В случае кодов Хэмминга центральное устройство обработки может быть вообще исключено, а объем буфера можно уменьшить до п ячеек. Многочлен локаторов (одиночных) ошибок задается равенством a(z) = l + aiZ, где = = И) (а). Общий вид декодера приведен на рис. 5.3.

Для БЧХ-кодов, исправляющих двойные ошибки, центральное устройство обработки должно выполнять некоторые вычисления в поле GF {Т"), а именно по заданным остаткам r(i) {х) и г(3) {х) от деления принятого слова на минимальный многочлен М) {х) элемента а и минимальный многочлен М) {х) элемента оно должно определить многочлен локаторов ошибок. Сначала находятся 5i = r(i) (а), = r) (а) и .з = г<){а). Затем нужно вычислить Оз {S-iS Sg)ISi или положить равным нулю, если Si и S3 равны нулю. Этот алгоритм декодирования позволяет исправлять двойные ошибки, однако, он не является полным. Код имеет смежный класс веса 3, который приводит к отказу декодирования.

148 Гл, 5, Двоичные циклические коды

В общем случае, если минимальный многочлен Aft) (х) элемента а является делителем порождающего многочлена, то центральное устройство обработки, в частности, вычисляет г() (х) - остаток от деления полученного слова на ilf<) (ж). Вычисления в центральном устройстве обработки начинаются с определения величины = = rW (а) и всех необходимых двоично сопряженных с 5 величин, таких, как Sk = 3% г-") (а") или = Si (а*"). Эти

вычисления выполняются сравнительно просто. Более тяжелой задачей является вычисление величин {о} по величинам {S,i}.

Представленный на рис. 5.14 декодер применим к произвольному двоичному циклическому коду. В качестве примеров мы рассмотрим два различных двоичных кода, исправляющих двойные ошибки. Вычисление {о} по величинам {S,} в этих примерах является сравнительно простым.

5.6. Пример

Построить кодер для двоичного циклического кода с блоковой длиной 23, порожденного минимальным многочленом для примитивного корня двадцать третьей степени из единицы. Построить декодер, исправляющий все сочетания из двух или меньшего числа искажен--; ных позиций.

Решение. Различные степени числа 2 по модулю 23 дают! числа 1, 2, 4, 8, 16, 9, 18, 13, 3, 6, 12. Так как мультипликативный!

Источник сообщений

5.6, Пример

вкл выкл

X X х" х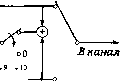

Рис. 5.17. Кодер для БЧХ-кода длины 23, исправляющего две ошибки.

порядок числа 2 по mod 23 равен И, то круговой многочлен (?<23) (ж)" распадается в произведение двух неприводимых двоичных многочле-1 нов степени 11. Если а - примитивный корень степени 23 из едини-i цы, то элемент а" не сопряжен с а, так что два неприводимых множи-; теля многочлена (?() (ж) являются взаимными многочленами. Исполь- зуя эту информацию и проводя умеренное число вычислений методом!

проб и ошибок, определяем, что делителями многочлена (?() (ж) являются ж" + ж» -Ь ж-Ь ж" -Ь ж -Ь ж -f 1 и ж" -Ь ж"» -f ж« + + ж -Ь ж* + ж + 1. Полагая g (ж) = ж" -Ь ж» -f- а; -f- ж« -f- ж -j-4- ж -t- 1, получим кодер, изображенный на рис. 5.17.

Работа декодера начинается с деления принятого слова на минимальный многочлен М() (ж) элемента а, который в данном случае равен многочлену g (ж). Так как 3 есть степень двойки по модулю 23, то (ж) = ilf() (ж). Таким образом, остаток г() (ж) от деления

на Af<*) (ж) равен многочлену И) (ж). Как только все деления закончены, декодер может определить Si = г() (а) и S = И*) (а) = = г(1) (а*). Зная Si и Sg, декодер может определить многочлен локаторов ошибок по обычной формуле для двоичных БЧХ-кодов, исправляющих две ошибки:

1, если ,?1= = О (класс смеж-

ности веса 0); l-fiZ, если Ss = Sl (включает

все классы смежности

(1.47) a(z)= ( веса 1);

i + SiZ+(si+- z, если SiO я (включает

,3 Ф SI все классы смежности

веса 2).

В рассматриваемом примере элементы поля GF (2) удобно задать в виде многочленов от а степени <; И, где а - корень порождающего многочлена. Вычисления SI и SJSi могут быть произведены с помощью методов, описанных в гл. 2. Затем, вычисляя а (а~), 1 = 0, 1, 2, . . ., 22, можно определить по процедуре Ченя все ошибки.

Необходимо отметить, что, хотя коэффициентами многочлена локаторов ошибок могут быть любые элементы поля GF (2), допустимыми взаимными корнями этого многочлена могут быть только корни двадцать третьей степени из единицы. Если же все корни многочлена локаторов ошибок попадают в множество корней двадцать третьей степени из единицы, то процедура приводит к ошибкам декодирования. В этом случае декодер знает, что в канале связи произошло более двух ошибок.

Хотя рассмотренный неполный алгоритм не позволяет исправлять все тройные ошибки, в разд. 15.2 будет показано, что возможна полная процедура декодирования, позволяющая исправлять все не более чем тройные ошибки.

5.7. Пример

Построить кодер для двоичного циклического кода с блоковой длиной 17, порожденного минимальным многочленом для примитивного корня семнадцатой степени из единицы. Построить декодер, исправляющий две или меньшее число ошибок в канале.

Решение. Различные степени числа 2 по модулю 17 дают числа 1, 2, 4, 8, -1, -2, -4, -8. Так как мультипликативный порядок числа 2 по модулю 17 равен 8, то круговой многочлен [х) распадается в произведение двух неприводимых двоичных многочленов, степень каждого из которых равна 8. Если а - примитивный корень семнадцатой степени из единицы, то а" сопряжен с а, так что каждый из двух неприводимых множителей многочлена является и своим взаимным. Поэтому можно заключить, что каждый: из неприводимых множителей представим в виде х -f Ах -f Вх -\- • + Сг" + Dx -f Сх -f Вх" + Лх -f 1. Деление этого многочлена] на X + 1 дает остаток D\ деление на х + 1 дает остаток (1 + -S +j + С) х + Dx + (1 + 5 + С); деление на {х -f 1) дает остаток j Dx* + (С + 1) г* + (Л + 5) х + (Л + 5) X + (С + 1). Так как; а; + 1 не является делителем искомого многочлена восьмой степе-) ни, то Z) = 1; так как х + а; + 1 также не делит этот многочлен,j то 5 + С = 1; так как и многочлен а;* + аг* + а: + а; + 1 erd не делит, то либо С = 1, либо А = В, либо оба эти равенства выпол-! няются одновременно. Таким образом, определяем делители {х) это х« + а; + а;« + а;* + а;2 + а; + 1 и а:« + х + а;* + х« + 1. Tai как последний делитель имеет меньше ненулевых коэффициентоВ то выбор его в качестве порождающего многочлена кода позволяе построить устройства с меньшим числом обратных связей. Полагаев g (х) = X* + х + X* + х 1. Читатель может без труда построит кодер для этого кода. Несложно и построение устройства делени принятого слова на ЛГ(х) = g{x) и выделения остатка г"(х). Име эти данные, декодер легко находит = /"(а). Для исправления дву ошибок необходимо также знать S. В данном примере, однакс* величина не может быть найдена. Так как число 3 не являете степенью 2 по модулю 17, то не является корнем порождающег многочлена кода. Ни одна комбинация проверочных позиций полз ченного слова не приводит к S. Для исправления двойных ошибо! декодер должен поступать иначе. Конечно, вообще говоря, anpnoj не очевидно, что данный код позволяет исправлять две ошибк Он, как и БЧХ-код с блоковой длиной 15, имеет только восемь пр верочных позиций. Восьми проверочных позиций достаточно дЛ исправления любых двух (или одной ошибки) в блоке из 15 двоичнь позиций, но консервативный читатель скептически отнесется к вс можности исправления с помощью восьми проверочных позиг любых двух ошибок в. блоке из 17 двоичных позиций. Тем не ме! даже скептики не могут отрицать такой возможности, пока не наг"

Ясно, что декодер не может выявить две ошибки, зная только S-. Так как он не может определить S, то ему необходима другая дополнительная информация. Декодер может определить S, = r(i) (а), 5, = r(ij (а*), = 7-(i) (а«), = = 7-<i> (a~i). Наиболее

полезной из этих величин является S.-. Если в канале произошли две ошибки, то Si и Si дают декодеру два независимых уравнения с двумя неизвестными:

Так как S i = {Х

= i + Siz + {sjsi) z

XyXiX, TO XiX = SJS.i и 0 (z) = Таким образом, в случае двух ошибок декодер может найти многочлен локаторов ошибок. В случае одной ошибки в канале а (z) = 1 + Sz. Следовательно, если произошла только одна ошибка, то декодер может ее исправить. Представляется возможным, что декодер может различать случаи одной и двух ошибок. Если в канале произошла одна ошибка, то S. = S~. В принципе такая ситуация возможна и при двух ошибках. Однако в этом случае 0(z) = 1 + Sz + Sy = {д + Sz) {д + Sz), где д GF (4) - примитивный корень третьей степени- из единицы. Тогда взаимными корнями многочлена о (z) являются локаторы

Xi = Si/d и = Si/d\ Но i/s i = XiXj{Xi + x) = s =

= Xi+Z2, так что XiX = (Z + Z)=S?. Так как Zj и Z-корни семнадцатой степени из единицы, ч<а S, 8\ж д = SylX также являются корнями семнадцатой степени из единицы. Но д = д" ф i. Из этого противоречия заключаем, что в случае двух ошибок в канале -1 фSl. Следовательно, все двойные и одиночные ошибки можно исправлять с помощью следующего алгоритма:

5.71. Алгоритм декодирования

1 , если 5i = .S i = 0;

D(Z) =

если iSj О и =

l + iz + -z2, если 8,фО, 5.1Ф<, 8.1Ф-.

Все вычисления алгоритма 5.71 выполняются в поле GF (2*). Читатель без труда сможет сконструировать соответствующие схемы.

5.8. Эквивалентность определений циклических кодов при помощи различных примитивных корней п-степени из единицы

Порождающий многочлен g (х) двоичного циклического кода с нечетной блоковой длиной п должен быть делителем многочлена

- 1 = [] (х - а*), где а - примитивный корень п-й степени