С (х) кратен g (х), то он удовлетворяет сравнению h (х) С (х) = = О mod (х" - 1). Более того, каждый кодовый многочлен С (х) удовлетворяет сравнению xh (х) С (х) s О mod (х" - 1) для любого Так как сумма проверочных соотношений опять задает проверочное соотношение и так как xh (х) является проверочным многочленом при любом /, то любой многочлен, кратный многочлену h (х) по модулю - 1, опять задает проверочный многочлен. Всего имеется 2ss(.x) многочленов степени <; п, кратных многочлену h {х) mod (х" - 1). Если бы код удовлетворял более чем 2"** проверочным соотношениям, то можно было бы найти более чем deg g (х) независимых проверочных соотношений, и тогда код должен был бы содержать больше чем deg g (х) проверочных позиций, что ведет к противоречию. Это приводит нас к следующему утверждению:

5.31. Теорема. Кодовыми многочленами линейного циклического кода с блоковой длиной п являются все многочлены, кратные одному порождающему {код) многочлену g (х). Множество проверочных многочленов этого кода состоит из всех многочленов, кратных проверочному многочлену h {х) = (х" - i)lg (х).

Например, проверочный многочлен исправляющего одиночн:в ошибки кода с и = 12 и порождающим многочленом g {х) = x + хi равен А (х) = х" -f + х -Ь X* + х + х + х + 1. Проверки, выписанные на предыдущей странице, очевидно, имеют вид

А«» {х) = h{x),

А<1> (х) = xh (х),

/1<2) (х) = z% (х),

АЗ) (х) = -М) А (х).

Другой пример дает исправляющий две ошибки циклический код с блоковой длиной /г = 15 и порождающим многочленом g (х)1- = (х + X + i) (x* + х + х + X + 1). Для него h (х) = (ж 1) X X {х + X -\- i) (ж* + х + I) = х + х + х + I. Строки обычной проверочной матрицы, задаваемой уравнением (5.21), очевидно, имеют вид

А<о> (х) = {х* + х + х -\- X -{- i) h (х), АЧ (х) = X {х* + х + х + X-\-1) h (х), А<2> (х) = х {х* + х + х + X + i) h (х), АЗ) (х) = (х" + 1) (х* + X* + х + X + 1) А (х), А<* (х) = (х + 1) (х* + X + i)h (х), А<« (х) = (х + 1) (х* + X -f 1) А (х), А« (х) = (х* + X + 1) А (х), /1<7> (х) = (х* + х2 + X + 1) (х* Ч- X + 1) А (х).

Как было показано в разд. 5.2, такая форма полезна, в частности, при вычислении величин и S, необходимых декодеру для отыскания локаторов ошибочных позиций. Однако нет никаких оснований использовать в декодере именно эту, а не какую-либо другую эквивалентную форму матрицы d. Любое множество из восьми независимых кратных многочлена h (х) будет порождать тот же самый

Источник сообщений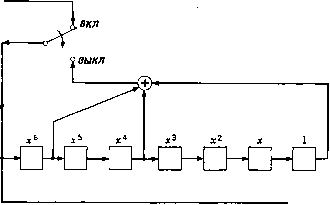

В канал

Р и с. 5.8. Кодер для циклического кода, основанный на проверочном многочлене.

код. Особенно простое множество образуют многочлены (х) =

= xh{x), i = 0, . . ., 7. Им соответствуют проверки 2 Cj+ih-,.i =

= О для 7 = 7, 6, . . . 0. Так как hj = \, то это эквивалентно равенствам

Cj=Cj.i, / = 7, 6, 5, 0.

Эти уравнения могут быть реализованы с помощью кодера такого же вида, как и на рис. 5.8, для Л (х) = 1 -f х* + х +

Сначала deg h (х) информационных символов посылаются одновременно в канал и в регистр сдвига. После этого источник сообщений отключается и осуществляется вычисление остальных п - - deg h (х) (проверочных) символов в соответствии с рекуррентным уравнением

deg л

С)= 2 Cj-.j/i(degft)-»-

Каждый из вычисленных таким образом проверочных символов передается по каналу связи и засылается обратно в регистр сдвига, так что при надобности он может быть использован для построения подпоследовательности проверочных символов. После передачи всех {п - deg h {х)) проверочных символов ключ возвращается в верхнее положение и начинается передача следующего блока.

Ясно, что в таком методе кодирования используется регистр, имеющий всего deg h {х) ячеек. При deg h < deg g кодер типа рис. 5.8 предпочтительнее кодера, изображенного на рис. 5.7.

5.4. Процедура Ченя

В разделе 5.1 мы видели, что, даже если локаторы опшбок декодеру известны, все же немедленное исправление ошибок вызывает определенные трудности. Оказывается, что проще подождать, пока искаженные символы будут выведены из буферного устройства, запоминающего принятое слово, а затем уже их исправлять.

Один из методов исправления ошибок, предложенный Ченем [1964], позволяет избежать отыскания явного решения алгебраического уравнения о {z~) = 0. Когда позиция с локатором Xi выводится из буфера, декодер вычисляет значение многочлена о (Zi), чтобы выяснить, обращается ли оно в нуль. Если а Ф О, то позиция с локатором Xi не изменяется, если же о (Z) = О, то в позиции с локатором Xi произошла ошибка, и она исправляется. Использование этого метода не ограничивается кодами, исправляю-; щими одиночные или двойные ошибки. Если в декодере известен

многочлен локаторов ошибок о (z) = 2 oi, корни которого взаимны

локаторам, то процедура Ченя может быть применена к каждому . из локаторов а", а"*, а~*, . . ., 1 для проверки, является ли ошибочным символ, выводимый в данный момент. Для БЧХ-кодов,. исправляющих двойные ошибки, многочлен локаторов ошибок о (z) может быть вычислен в соответствии с уравнением (1.47); для БЧХ-кодов, исправляющих ошибки более высокой кратности, процедура вычисления многочлена локаторов ошибок описана в гл. 7. При известных коэффициентах Oj, g, . . ., Ot процедура Ченя;

сводится к следующему. Сначала декодер вычисляет ст (а) = 2 ojCvi

t .5

затем о (а)= 2 <7i«% о («*) = S ojC** и т. д. Для быстрого вычис-

ления этих величин в декодере используется f + 1 регистров. HaN к-ш шаге вычисления в этих регистрах записаны величины 1, аа*,:! аа, OTgO, . . ., ста*. Величина а (а) получается суммирова-Т нием содержимых этих регистров. Для перехода к (А; + 1)-му шагу регистр, содержащий оа, умножается на а, регистр, содержащий;

жается на а . Все эти умножения в GF (2"-) могут осуществляться одновременно. Для относительно малых значений t и m целесооб разно встроить схемы, реализующие умножение регистров, содержа,

Ota ; на постоянные 1, а,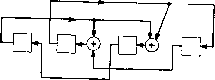

Рис. 5.9. Схема умножения на а. Р и с. 5.10. Схема умножения на а.

В один временной цикл. Например, умножение в GF (2*) на элемент а, такой, что а* = а -f 1, может быть выполнено с помощью схемы, изображенной на рис. 5.9. Умножение на элемент а* может быть выполнено с помощью схемы, изображенной на рис. 5.10. Процедура Ченя реализуется с помощью схемы, представленной на рис. 5.11.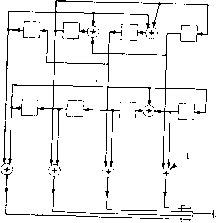

OiO,, умножается на а*,

регистр, содержащий Ojo", умно»-

Прибавить X выходу буферного устройства

Рис. 5.11. Схема Ченя для кода, исправляющего две ошибки.

Сначала в верхнем регистре схемы рис. 5.11 записан элемент а в нижнем а. В каждом временном цикле верхний регистр умножается на а, анижний на а. После к временных циклов верхний регистр содержит оа?, а нижний оа. В сумматоре вычисляется величина а (а) = 1 + ста -Ь 02а*. Если эта величина равна нулю, То а" является взаимным корнем многочлена локаторов ошибок; к ошибочному символу с локатором а", выводимому в данный

момент из буфера, добавляется единица. Если о (а) Ф О, то а" не является взаимным корнем многочлена локаторов ошибок и позиция с локатором выводится из буфера без изменений.

При больших значениях t ж т стоимость оборудования, выполняющего умножение на а в GF (2") в один временной цикл, стано-; вится значительной. Для средних значений t умножение на а можно

t вспомогательных умножителей

К выходу буфера

Главный накопитель

Сигналы

управления "

Рис. 5.12. Общий вид схемы Ченя для кода, исправляющего t ошибок.

осуществлять как i-кратное умножение на а. Для реализации тако1 способа требуется только регистр умножения на а, но для большт" значений t это приводит к большому числу сдвигов. В этих случае обычно более экономным является использование т временных ци лов для каждого из умножений, которые могут быть выполне! одним из методов, описанных в разд. 2.4. Целесообразно выполнг все t умножений одновременно. На рис. 5.12 приведена схема, peaj зующаячтакое умножение. В этой схеме используется один главг блок управления и t идентичных вспомогательных умножитег один из которых изображен на рис. 5.13. В начальный момент i вый вспомогательный накопитель содержит а; первый вспомо тельный регистр осуществляет умножение на а; второй вспомо! тельный накопитель содержит о; второй вспомогательный per""

осуществляет умножение на а, . . ., i-й вспомогательный накопитель содержит Oi\ i-й вспомогательный регистр осуществляет умно-н«ение на a. Главный блок управления посылает на все вспомогательные умножители идентичные сигналы управления, согласно которым содержимое каждого вспомогательного накопителя переводится в умножаемый регистр, умножается на соответствующий множитель и новое произведение записывается обратно в накопитель.

Вспомогательный накопитель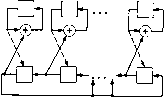

Регистр множимого

Регистр множителя

Рис. 5.13. Типичный вспомогательный умножитель.

В главном сумматоре вычисляется сумма содержимых всех вспомогательных накопителей, которая помещается затем в главный накопитель. Эта величина и есть а (а). Продолжая эту процедуру, последовательно подсчитаем а (а"), . . ., о (а-), а (1). Позиция с локатором а*, выводимая из буферного регистра, исправляется тогда и только тогда, когда а (а~) = 0.

5.5. Описание общей схемы декодера для произвольного циклического двоичного кода

Общая схема декодирующего устройства для произвольного двоичного циклического кода показана на рис. 5.14. Декодер состоит n:j четырех основных частей: буферного регистра, содержащего 2п ячеек, регистров сдвига, осуществляющих деление принимаемого слова на каждый из неприводимых множителей порождающего многочлена, центрального устройства обработки в поле Галуа (определение {oj по {Si}) и схемы, реализующей процедуру Ченя. В типичный момент времени содержимое буферного устройства состоит из Ц)ех частей, показанных на рис. 5.15. Первые i ячеек содержат пер-Bj,ie i позиций вводимого слова; следующие п ячеек буфера содер-

) Или Gi-оператора.- Прим. перев. 10-658