Сп-1, Сп-2, . . ., поступают одновременно в канал и в регистр с обратной связью. Затем все ключи переключаются в свое нижнее положение. При этом источник отключается, на вход обратной связи

ВЫКЛ. о

В канал

Рис. 5.5. Кодер для кода Хэмминга.

ничего не подается и содержимое регистра сдвига поступает в канал связи. После передачи по каналу всех позиций регистра сдвига ключи возвращаются в верхнее положение и начинается передача следующего блока.

5.2. Переупорядочение столбцов проверочной матрицы двоичных БЧХ-кодов, исправляющих двойные ошибки

Упорядочение позиций кода в соответствии со степенями примитивного элемента поля обладает многими преимуществами и в случае БЧХ-кодов с исправлением многих ошибок. Для двоичных кодов, исправляющих двойные ошибки, вторая группа из т строк проверочной матрицы SB строится таким образом, что каждый стол- , бец является кубом локатора, записанного в этом столбце в первых т строках матрицы. Таким образом, матрица содержит п столбцов, 2т строк и имеет вид

<0 =

(5.21)

Например, если /г = 15 и а -корень многочлена ж* + а;--1, т©

"О О 0-1 О О 1 1 О 1 О 1 1 1 1] 0010011010111 О 010011010111100 100010011010111

011110111101111 001010010100101 000110001100011 100011000110001

Синдром S = JR содержит 2т координат. Первые т координат дают Si, сумму локаторов ошибочных позиций; вторые т координат синдрома дают S, сумму кубов локаторов искаженных позиций.

Если принятый вектор представить многочленом R (х) = 2 i*,

К) = л (а) и 3 = Д (а*). Принятый вектор позволяет вычислить каждую из этих сумм в отдельности. Для вычисления S- надо разделить R (х) на минимальный многочлен Tlf) (х) элемента а п найти остаток от деления г*) (х). Тогда имеет место равенство Sx = /-(i) (а). Для вычисления S надо разделить R (х) на минимальный многочлен 7lf(*) (х) элемента а, найти остаток от деления г() (х) и вычислить затем = г*) (а). В общем случае вычисление 5з по г() может потребовать просчета не более чем т проверочных соотношений с не более чем т входами i).

В рассматриваемом примере минимальным многочленом для а* является ж* Н- ж* -Ь х а; -Ь 1. Многочлены т-) (х) и г(*> (х) могут быть получены с помощью схемы, изображенной на рис. 5.6. Получаемые декодером из канала связи позиции подаются в 15-позицион-ный буферный регистр, изображенный нарис. 5.6 горизонтально вверху. После приема всех 15 позиций блока в буфере оказывается записанным многочлен R (х), представляющий принятое слово. Одновременно с буферным регистром принятое слово поступает еще в два регистра, обратные связи которых подобраны в соответствии с минимальными многочленами для а и а*. Начальное состояние обоих регистров является нулевым. При вводе позиций из канала эти регистры осуществляют деление соответственно на минимальный многочлен Л/1) (х) элемента а и минимальный многочлен ilf (х) элемента а*. При окончании приема входного блока из 15 позиций в регистрах содержатся соответственно остатки г) (х) д г) (х).

Степенные суммы S-, S и S вычисляются по остаткам r(i) (х) и г*) (х) путем «матричного» умножения, изображенного на рисунке с помощью вертикальных регистров и вентильных схем. Матрица, используемая для получения S- по г) (х), оказывается единичной; поэтому S-i просто совпадает с г) (а). Однако вычисление 8,= = г) (а) и Ss = г(*) (а*) требует более сложной схемы. Связи для этих матриц умножения легко могут быть получены из первых т столбцов расширенной матрицы SB, которые для рассматриваемого примера имеют вид

0 0 0 1

laaa < q 1 О О 10 0 0

) можно получить акже путем деления R(x) на il/<i)(x). Этот способ позволяет обойтись без специального регистра, выполняющего деление на (), но требует намного большего числа сдвигов.

а:13 Д.14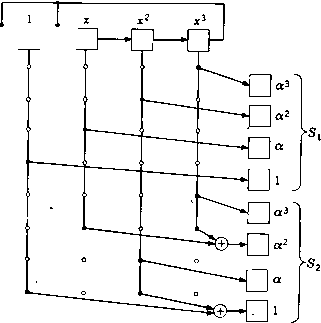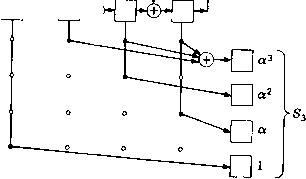

1 а2 а* а"

1аЗа« а»-

0 0 0 1 0 10 1 0 0 10 10 10

0 111 0 0 10 0 0 0 1 10 0 0

Рис. 5.6. Первая часть декодера для БЧХ-кода, исправляющего две ошибки.

Так как элемент сопряжен с а, то он имеет тот же минимальный многочлен и, следовательно, может быть вычислен по тому же остатку, что и S. Поэтому в общем случае можно не включать в проверочную матрицу, хотя это и не принесет вреда. Расширенная проверочная матрица (включающая в себя, помимо самих локаторов и их кубов, квадраты локаторов) имеет больше строк, чем обычная проверочная матрица. Однако дополнительные строки являются линейными комбинациями первых т строк, и ранг расширенной проверочной матрицы равен рангу обычной проверочной матрицы. Проверочная матрица может быть расширена еще больше, если добавить сопряженные с Зи Sg, т. е. Si,, Sg или Sg. Суммы SiVi Sg могут быть вычислены но остатку г) (х), & S - по остатку г (х).

Кодирование начинается с задания информационных символов С„ 2, . . ., С2т- После ЭТОГО кодер должен найти такие символы Cjm-i, 2-21 • • •> Со, чтобы розультирующий многочлен

2С;а;* удовлетворял уравнениям С (а) = О и С (а*) = 0. Первое

ИЗ этих условий выполняется тогда и только тогда, когда С (х) кратен минимальному многочлену элемента а, а второе - тогда и только тогда, когда С (х) кратен минимальному многочлену элемента а. Так как многочлен С (х) кратен обоим этим неприводимым многочленам, то он кратен и их произведению, которое мы обозначим через g (х). Выбрав для исправляющего двойные ошибки двоичного БЧХ-кода с блоковой длиной 15 в качестве а корень многочлена

+ х + 1, получим, что минимальным многочленом для является х* + х+ х+х +1, й g (х) ={х* + х+ i) {х + х + х + х+1)== = х + ж + ж* + * + 1- Кодирующее устройство может быть построено по тому же самому принципу, что и кодер для кодов, исправляющих одиночные ошибки. На рис. 5.7 приведена схема Кодера для рассматриваемого частного случая.

Семь информационных позиций посылаются одновременно в канал и регистр сдвига. После этого ключи возвращаются в нижнее положение. Восемь проверочных позиций посылаются в канал из регистра Сдвига, после чего в нем устанавливаются нули. Затем к началу передачи нового блока ключи опять переводятся в верхнее положение.

Для данного кода существует и другой кодер, реализация которого основана на регистре сдвига только с семью ячейками. Для понимания принципа действия этого кодера полезно обратиться к изучению циклических кодов.

Источник сообщений

вкл. выкл.о

в канал

Рис. 5.7. Кодер для циклического кода, основанный на порождающем многочлене.

5.3. Общие свойства циклических кодов

Для БЧХ-кодов, исправляющих одиночные ошибки и для БЧХ-кодов, исправляющих двойные ошибки, нам удалось найти многочлен g {х), обладающий тем свойством, что двоичный многочлен С{х) степени <in задает кодовое слово тогда и только тогда, когда С{х) кратен g{x). Этот многочлен g(x) называется порождающим многочленом циклического кода. Разделим многочлен С (х) на многочлен g{x) h{x), кратный g(x), и пусть q{x) - частное от деления, а г{х) - остаток, так что С = qgh + г. Многочлен С {х) делится на g{x) тогда и только тогда, когда г{х) делится на g{x). Таким образом, если многочлен С {х) задает кодовое слово, то любое кратное С {х) по модулю g {х) h {х) задает другое кодовое слово. В частности, если g ix) является произведением различных неприводимых многочленов, степени которых делят т, то g{x) делит а;"- - 1 = = х" - 1. Выбирая h{x) = (ж" - \)lg{x), заключаем, что если многочлен С {х) задает кодовое слово, то и любое его кратное по модулю л;" - 1 задает кодовое слово. Назовем й.(ж) проверочным многочленом,-

Если многочлен С {х) = Cq + С-х + Сх . . . C„-ix"-i умно-< жается на х по модулю х" - 1, то результат равен C.j + . + СоХ СхХ + . . . + С„ 2х""1. Таким образом, ясно, что кодовое, слово, заданное многочленом хС{х) по модулю х" - 1, является! циклическим сдвигом кодового слова, заданного многочленом С (a;).j Так как каждый циклический сдвиг кодового слова приводит, такимГ образом, опять к кодовому слову, то код естественно назвать цикли-1 ческим. Очевидно, что если g (х) - произвольный делитель многочле-! на х" - 1, то множество кратных многочлену g {х) по модули!

ж" - 1 образует линейный циклический код. Это справедливо и в том случае, когда число п + 1 не является степенью двойки.

Наоборот, пусть линейный циклический код задается как некоторое множество многочленов по модулю х" - 1. Тогда код содержит все к-е циклические сдвиги хС (х) mod (х" - 1) произвольного кодового многочлена С{х). Так как сумма кодовых слов линейного кода принадлежит коду, то код содержит все кратные многочлена С (х) по модулю х" - 1. Используя алгоритм Евклида, н.о.д. многочленов С" (х) и х" - 1 можно записать по модулю х" - 1 как кратное многочлена С (х). Следовательно, линейный циклический код содержит н. о. д. каждого кодового многочлена и многочлена х" - 1. Обозначим через g (х) кодовый многочлен наименьшей степени. Тогда g (х) делит х" - 1 и любой кодовый многочлен.

Таким образом, линейный циклический код состоит из всех многочленов, кратных некоторому порождающему многочлену g{x) по модулю х" - 1, причем" g (х) I (х" - 1).

Многочленная запись оказывается также полезной при задании проверочной матрицы Se- Например, если а - корень многочлена X* + X -Ь 1 и

< = 111 а I I а» I а* 1 I «в 1 а I а81 а» I а"» I а" I 1

0 0 0 1 0 0 1 1 0 1 0 1 1 1 1 001001101011110 010011010111100

1 0001001101011 1.

то строки матрицы® можно задавать многочленами (х), А) (х), (х) и /1(3) (х), где

fe«"(x) = х" + х8 + х + х + х" + х + X + 1, /ii(x) = х12 + X» Ч- Х + Х« + X* + х + х2 + X, h>{x) = х1з + х!" + X» -f х + х + X* + а; + х, /1<3)(х) = х" Ч- хо + х + хв + X* Ч- х« + X + 1.

Предположим, что получено слово С = [Со, Ci, С, •, 14]. Скалярное произведение С и первой строки матрицы SS равно С3 + + Сб + С7 Ч- Сэ + Сц Ч- Ч- Ч- Ci4. Так как наивысшей степенью х в многочлене С (х) является крайний правый член, а в многочлене Л<<" (х) - крайний левый член, то скалярное произведение вектора С и первой строки матрицы SB равно коэффициенту при х* в произведении многочленов А<о(х) С (х), редуцированном по модулю х" - 1. Аналогично, скалярное произведение кодового вектора С и второй строки матрицы S6 равно коэффициенту при х* в произведении многочленов /г (х) С (х) и т. д.

Многочлен А(х) = (х" - 1)/ (х) обладает тем свойством, что W g (х) = Omod (х" - 1). Так как каждый кодовый многочлен