
 |
|
Главная страница Программы проектирования [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [ 94 ] [95] [96] [97] [98] [99] [100] емых значений путем целенаправленного изменения заданных параметров системы. Решение этой задачи осуществляется с помощью поисковых алгоритмов оптимизации, описанных в гл. 11. Критерии качества, характеризующие быстродействие, точность, устойчивости, энергетические затраты и т. д., формируются по результата.м моделирования или другим видам анализа, выполняемым комплексом. Наличие специальных типовых блоков позволяет сформировать такие критерии, как перерегулирование, время переходногр процесса, ошибку при типовых воздействиях и др. Могут бытк также сформированы критерии качества на основе требовани! к частотным характеристикам и расположению корней. Задание на оптимизацию включает описание критериев качества и оптивцизируемых параметров. Оптимизируемыми параметрами могут \быть любые параметры любых блоков структурной схемы. Для проведения оптимизации необходимо задать начальные значения оптимизируемых параметров, от выбора которых во многом зависит успешность оптимизации. При неудачном выборе можно вообще не получить ожидаемых результатов. Поэтому перед началом оптимизации рекомендуется приближенно оценить оптимальные значения параметров на основе анализа упрощенной модели и выбрать их в качестве начальных. 12.3. ПРИМЕРЫ ИССЛЕДОВАНИЯ СИСТЕМ С ПОМОЩЬЮ КОМПЛЕКСА ПРОГРАММ Приведем примеры решения задач анализа и параметрической оптимизации автоматических систем с помощью описанного комплекса программ. Пример 1. Определить параметры К\, Кг системы на рис. 12.1 таким образом, чтобы при единичном входном воздействии ы(/) = 1(/) перерегулирование не превышало 2%, а время переходного процесса по уровню 0,98 было минимальным. Произвести маделирование системы с начальными и полученными оптимальными значениями параметров. Начальные значения параметров задаем 10 0,8 0,6 0,1* 0.2 О
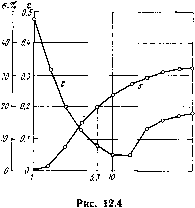 Kfl, KfO. Входной описок заданий для решения перечисленных женный комментариями, имеет вид дач, снаб- с ввод СТРУКТУРНОЙ сши 1 с-----------------------
с МОДЕЖРОВАНИЕ С J*>4A*HUMM ЗНАЧЕНИЯМИ ПАРАМЕТРОВ 3 5 0.1 0 0 0 5 30 0 С 0ГГИ»«13АЦИЯ 4 5 0 0 0.02 1 200 41 1.02 42 0 0 15 1 0 0.5 0 10 15 2 0 0.5 0 10 0 С МОДЕЛИРОВАНИЕ С ОПТИМАЛЬНЫМИ ЗНАЧЕНИЯМИ ПАРАМЕТРОВ. 3 5 0.1 0 0 0 5 30 0 Блоки с номераин 41 и 42 вырабатыгаают критерии качества: маконшальное значение выходной переменной время переходного процесса. В заданиях «а моделирование )жазывак>тся: номер задания (3), время моделирования (5), шаг печати (0,1). Три последующих нуля означают, что максимальный и минимальный шагн интегрирования и относительная точность выбираются програ1Ммой по умолчанию. Далее следует вид вывода (5) и номер выводимого блока (30). В задавая на оптим;изащию в первой строке перечисляются: номер задания (4), время моделирования при расчете критериев (5), максимальный и минимальный шаги интегрирования (задаются по умолчанию), относительная точность оптимизации (0,02), вид вывода (I-вывод значений критериев и параметров в промежуточных точках), макоимальное число моделироваяпй прн оптимизации (200). Во второй строке перечисляются номера блоков, выходы которых являются критериями качества, а также задаются требования к крите-риим: выход блока 41 не должен превышать 1,02, а выход блока 42 должен быть минимальным. В последующих двух строках задаются оптимизируемые параметры (параметры 1 и 2 блока 15), начальные шаги по ним (0,5 для каждого параметра), минимальные и максимальные значения (О и 10 для каждого параметра). В результате решения задачи оптимизации получаем: /Ci=3,82, /(2=1.04. Оптимизация потребовала 1 мин 52 с времени ЭВМ ЕС1033. При этом система моделировалась 144 раза. На рис. 12.3 приведены кривые переходного процесса при начальных (/) и полученных оптимальных (2) значениях параметров. Пример 2. Структурная схема автоматической системы приведена на рис. 12.2. Критериями качества являются перерегулирование при единичном входном воздействии ti{t)=!l{t) я ошибка слежения при гармоническом входном воздействии «(<)-= sin 0,5/. При заданном /С2=0,5 требуется построить зависимости выбранных йритернев от параметра Ci. у Требуется тайнее определить Ki таким образом, чтобйк при перерегулировании, не превышающем 20%, ошибка слежения была минимальной. o.s Для решения\этой задачи восполь-зуемся многовариатным анализом. Полученные кривые зависимостей перерегулирования а н ош11бки слежения е от параметра К\ приведены на рис. 12.4. Из этого рисунка видно, что заданным требованиям удовлегворяет /Ci=6,3. Кривая переходного процесса при выбранном значении Ki приведена на рис. 12.5. В ходе выполнения мнрговариантного анализа система моделировалась 11 раз при единичном и гармоническом входных воздействиих. Это потребовало около 2 мин времени ЭВМ ЕС 1033. 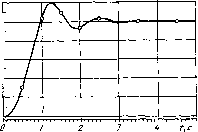 Рис. 12.5 HO,Zp 0,03 D,25p y(t) 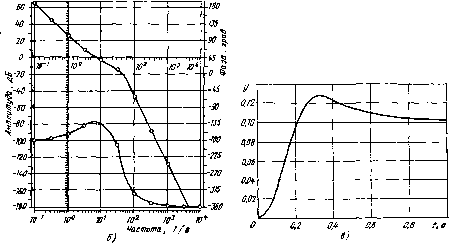 [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [ 94 ] [95] [96] [97] [98] [99] [100] 0.0294 |