Здесь Уи ..., Ут - выходные сигналы всех блоков структурной схемы; «1,..., щ - внешние воздействия. Отметим, что система (1.40) сильно разрежена и каждая ее строка содержит, как правило, от двух до четырех ненулевых элементов.

Передаточную функцию от /-го входа к выходу i-ro блока можно найти по системе уравнений (1.40), воспользовавшись правилом Крамера:

aiiip) ... bijip) ... aim(p) ami(p) ... bmjjp) ... amm(P)

aii(P) . aim(p) ami(p) . . . ammip)

Таким образом, задача нахождения передаточных функций сводится к вычислению определителей сильно разреженных полиномиальных матриц.

Приведенный здесь алгоритм позволяет по заданной структуре матрицы, т. е. по расположению ее ненулевых элементов, построить расчетный граф для вычисления определителя. Под расчетным графом будем понимать ориентированный граф, отражающий последовательность действий при вычислении определителя.

Рассмотрим работу алгоритма на конкретном примере. Будем вычислять определитель матрицы

О а

Си О О

«32 й;

О а44

(1.41)

Раскладывая определитель матрицы (1.41) по элементам первой строки, имеем А =aiiMii-ai2Mi2-аМм, где Мп, M12, Л1,4 - дополнительные миноры соответствующих элементов. В соответствии с правилом знаков, берем знак «-Ь», если индекс столбца четный, и «-», если индекс столбца нечетный. Далее будем аналогично раскладывать миноры Мп, п, ЛГи по элементам строки 2 и т. д. В конце концов дойдем до последней строки и сможем сформировать выражение для определителя через элементы матрицы.

Формирование расчетного графа удобно представить в виде таблицы (табл. 1.1), каждая строка которой соответствует строке матрицы (1.41). Заполнив первые две колонки таблицы, мы полностью описали расположение ненулевых элементов в матрице. В третьей колонке таблицы будем формировать расчетный граф. Каждая его вершина соответствует элементу матрицы, по которому раскладывается определитель. Примем вес вершины равным значению этого элемента, взятому с тем знаком, с которым он входит в определитель. Путем в расчетном графе будем

считать последовательность вершин, связанных дугами и упорядоченных направлениями дуг.

В третью колонку табл. 1.1 запишем индексы столбцов элементов, по которым раскладывается определитель, причем с теми знаками, с которыми соответствующие элементы входят в определитель. Формально действия выполняются следующим образом. В первую строку таблицы переписываем числа, перечисленные во второй колонке, меняя знак числа на «-», если оно четное. В каждой последующей строке под каждым числом предыдущей строки записываем числа из второй колонки, кроме тех, которые встречались в пути, приводящем к этому числу. Знак числа определяем следующим образом. Берем последовательность

1, 2..... N {N - значение числа, для которого нужно определить

знак), вычеркиваем из нее все числа, которые уже встречались в вышележащей части пути. Если осталось нечетное количество чисел, берем знак «-Ь», а если четное, то «-». После заполнения очередной строки соединяем элементы этой строки с соответствующими элемевтамн вышележащей строки стрелками, направленными сверху «низ.

Если в двух путях, лежащих выше данной строки, содержатся одни и те же индексы столбцов, то зпи пути входят в один минор верхних строк. Тогда в очередной строке таблицы эти пути объединяются так же, как пути 1-2-3 и -2-1-3 в табл. 1.1. Величиной пути в графе назовем произ-ведеиие весов вершин, входящих в этот путь. Напр1имер, величина пути 1-2--4-3 в табл. 1.1 равна аиа22{-аз4)а4з- Бели путь начинается в верхней строке таблицы и кончается в нижней, то его 1величина равна произведению элементов матрицы, входящему в определитель. Если путь не Рис. 1.2 доходит до нижней строки (будем на-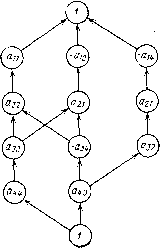

зывать такой шуть тупиковым), то проиэведвиие соответствующих элементов не содержит1ся в определителе, и этот путь следует от--бросить. В табл. 1.1 тупиковыми являются пути -4-1---3 и 4 2-3.

Определитель матрицы равен сумме величин всех нетупиковых путей сформированного расчетного графа. Направления дуг показывают последовательность вычислений. Отметим, что изменение направлений всех дуг на противоположные не изменит окончательного результата, однако такой прием позволяет избавиться от тупиковых путей.

Для формирования окончательного расчетного графа изменим направления дуг, отбросим тупиковые пути, запишем в вершинах их веса и добавим начальную и конечную вершины. Сформированный расчетный граф показан на рис. 1.2. По этому графу легко вычислить значение определителя. Вычисление начинаем с нижней вершины. В каждой вершине осуществляется сложение поступающих на нее входных данных и умножение полученной суммы на вес вершины. В результате на выходе верхней (конечной) вершины получаем значение определителя, равное A = (aiia22- -«1221) (азза44-aziuiz)-ацацазчац.

Указанные выше действия по формированию расчетного графа легко формализовать, если выбрать достаточно удобную структуру далных для хранения исходной матрицы и промежуточных результатов. Для этой цели в программе, реализующей приведенный алгоритм, используется связанный список [84].

1.6. РЕАЛИЗАЦИЯ ПЕРЕДАТОЧНОЙ МАТРИЦЫ В ВИДЕ УРАВНЕНИЙ СОСТОЯНИЯ

В § 1.3 были рассмотрены алгоритмы формирования уравнений состояния по заданной передаточной матрице с общим знаменателем в тех случаях, когда число входов (или выходов) равно единице. Порядок получаемых уравнений состояния был равен степени передаточной матрицы (максимальной степени полиномов ее числителей и знаменателя). Однако в общем случае передаточную матрицу, приведенную к общему знаменателю, не всегда можно реализовать в виде уравнений состояния, порядок которых равен степени передаточной матрицы. Например, для реализации передаточной матрицы W(p)=-

1 Р 1 Р

достаточно од-

ного интегратора, а для реализации передаточной матрицы W(p)=- "

1 О о 1

необходимо два интегратора, хотя степень обоих передаточных матриц равна единице.

В этом параграфе рассмотрены необходимые и достаточные условия [75] реализуемости правильной передаточной матрицы с общим знаменателем в виде уравнений состояния, порядок которых не превышает степени передаточной матрицы. Эти условия состоят в том, что произвольный минор k-TO порядка матрицы