Начали

у=х+Дх

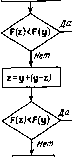а0,5а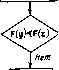

а-да

y=x-j3(z-x)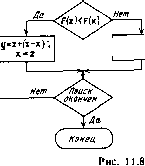

Пусть Н - симметричная положительно-определенная матрица. Будем строить последовательность матриц Но = Н, Hj,, ..., каждая из которых получается из предыдущей путем выполнения следующего преобразования:

Hft = PftAfeHft ,AftPft, (11.5)

где Ah - диагональная матрица с элементами ki-=\lY{ha - диагональные элементы Hft ij; Р -некоторая ортогональная матрица. После умножения матрицы Hft i слева и справа на As получаем матрицу с единичными диагональными элементами. Можно надеяться, что при подходящем выборе ортогональных матриц Pft матрица Ни будет стремиться к единичной. На этом, в частности, основан метод вращений для расчета собственных значений симметричных матриц [20].

Перейдем теперь к задаче поиска минимума функции нескольких переменных. На k-м этапе поиска будем поочередно минимизировать функцию в направлениях векторов si,..., Sn, которые представляют собой столбцы матрицы S. Для нахождения точки минимума в направлении s, будем использовать квадратичную интерполяцию по трем равноотстоящим точкам х-as,-, х, x+asj. Одновременно для каждого направления вычислим

h = a{f (x+asi) +/ (x-asi) -2f (x) (И .6)

После выполнения серии спусков преобразуем матрицу S по формуле

где A/i -диагональная матрица, элементы которой определяются из (П.6); Pft -некоторая ортогональная матрица. Для квадратичной целевой функции матрица SfftHSh, где Н - матрица Гессе, совпадает с матрицей Н, полученной при выполнении преобразований (11.5). Таким образом, при надлежащем выборе матриц Р для квадратичной функции получаем S/iHSft-I, и направления поиска приближаются к сопряженным. В предлагаемом алгоритме матрица Pft одинакова на всех эта-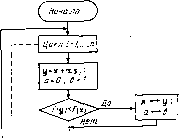

о 3 я р з: м

Ь: ~ = 3- £«.

Значение функции по алгоритму

a=f(y)*f(x)-2f{A

Ва+у(а.в)\ 5; = Л-5г

Не.чдера-Мида

24,2 1,6

4,610-*

4,2.10-

24,2 0,0051 1,8-10-» О

24,2

0,11

6,2-10-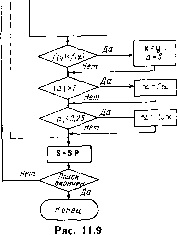

пах и определяется по формуле (11.4). Схема алгоритма представлена на рис. 11.9.

Все четыре алгоритма были проверены на ряде тестовых задач и показали высокую эффективность. Например, результаты минимизации тестовой функции Розенброка

f (X) = 100 (х2-х)2+ {1-х,У (11.7)

из начальной точки Хо=(-1,2; l) приведены в табл. 11.1. Для сравнения в таблице приведены результаты, полученные алгоритмом Нелдера - Мида, одним из наиболее эффективных алгоритмов поисковой оптимизации.

11.4. ПРОГРАММЫ ОПТИМИЗАЦИИ

Описанные выше алгоритмы реализованы в подпрограммах P0ISK2 и P0ISK4. Подпрограмма P0ISK2 реализует алгоритм деления шага пополам при п=1 и алгоритм 2 при п>1, подпрограмма P0ISK4 - алгоритм квадратичной интерполяции при л= = 1 и алгоритм 4 при л>1.

Подпрограмма P0ISK2

Назначение: оптимизация векторной целевой функции.

Обращение: CALL P01SK2 (X, FX, N, М, DX, EPS, NFEMAX, FUN, COMP, lOUT, OUT). Параметры:

X - начальное значение вектора оптимизируемых параметров (на

входе), полученное оптимальное значение вектора параметров (на выходе),

эиачеиие векторной целевой функции при полученных оптимальных значениях параметров, размерность вектора X,

размерность вектора FX,

вектор начальных приращений по параметрам, относительная погрешность нахождения оптимальной точки, рекомендуется задавать в диапазоне 10-... 10-, максимальное число вычислений целевой функции, имя подпрограммы вычнсления векторной целевой функции; ее параметры: X - вектор параметров, FX - значение векторной целевой функции в точке X,

имя подпрограммы сравнения значений векторной целевой функции; ее параметры: X, Y - векторы параметров; FX, FY - значения векторной функции в точках X, Y; N - размерность векторов X, Y; М - размерность векторов FX, FY; 1С - целое число, равное 1, если значение целевой функции в точке X лучще, чем в точке Y, равное 2, если значение целевой функции в точке X хуже, чем в точке Y, равное 3, если следует закончить оптимизацию, IOUT - целое число, равное О, если промежуточные результаты не выводятся, и 1, если следует выводить промежуточные результаты,

N М DX EPS

NFEMAX FUN

COMP -