
 |
|
Главная страница Программы проектирования [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [ 87 ] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] один из пробных шагов оказался удачным, производим спуск в выбранном направлении с возрастаюш,им шагом. В результате получаем новую точку поиска Xj+i =x,+VjSj, причем при неудачных пробных шагах уг = 0. Корректировка матрицы А осуществляется по формуле A,+, = A, + (pi-l) Si sjAi (11.3) где рг=0,5, если у!=0, и Рг=уг, если угО. При этом преобразовании эллипсоид растягивается, если pj>l, или сжимается, если Р,<:1, в направлении вектора s,, оставаясь неизменным в направлениях, ортогональных s;. Действительно, рассмотрим два вектора Vi = Ail, V2 = Ai+i, где I - произвольный единичный вектор. Разложив каждый из них на две составляющие: параллельную и ортогональную Sj - и используя (11.3), получаем: Vi = asi-bp, sjp=0; V2 = Vi + (р,- 1)= p. a + p. Сравнивая эти разложения, видим, что составляющая, параллельная s,, вектора V2 в Pi раз больше, чем вектора Vi, а составляющая, ортогональная s,, осталась без изменений. Деформация эллипсоида при преобразовании (11.3) проиллюстрирована на рис. 11.4. Схема алгоритма случайного поиска с адаптацией представлена на рис. 11.5. Отметим, что спуск в выбранном направлении осуществляется весьма грубо. Попытки производить одномерный поиск более точно приводили к снижению эффективности алгоритма. Алгоритм 2. Направления поиска на k-m этапе задаются матрицей Sk- На очередном этапе производится серия спусков в направлениях векторов si, Sn, представляющих собой столбцы матрицы Sft. Векторы перемещений на каждом из спусков равны соответственно yiSi, ynSn. После выполнения спусков матрица направлений преобразуется по формуле Sft-t-i = SfeAftPfe, где Aft - диагональная матрица, элементы которой равны Лг = уг, если fiO, и Я, = 0,5, если уг = 0; Pk - ортогональная матрица. Умножение на ортогональную матрицу необходимо для изменения набора направлений поиска. Если на всех этапах Pft = I, то направления поиска не изменяются от эта-Рис. 11.4 па к этапу и мы имеем алгоритм покоор- 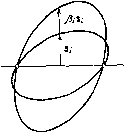 динатного спуска. Очевидно, что выбор матриц существенно влияет на эффективность поиска. Было испытано несколько различных способов выбора ортогональных матриц Pft, в том числе и случайный выбор. Лучшим оказался способ, при котором все матрицы Р равны между собой и определяются в виде п- 1
(11.4) Схема алгоритма приведена на рис. 11.6. Алгоритм 3. Этот алгоритм основан на прогнозировании новой точки поиска по предыдущим подобно тому, как это делается в методах, использующих экстраполяцию (методе конфигураций). Рабочий шаг поиска (рис. 11.7) состоит из шага экстраполяции (/) и уточняющего поиска (2). Экстраполяция производится по текущей точке поиска и предыдущей точке, уточняющий поиск-как спуск в случайно выбранном направлении. Как показали эксперименты, этот спуск должен быть достаточно грубым. Если очередной рабочий шаг оказался неудачным, шаг экстраполяции уменьшается и изменяется его направление на противоположное. Такой прием оправдан, если движение происходит вдоль оврага и на очередном шаге мы пропустили точку минимума. Тогда продолжение движения в выбранном направлении будет удалять нас от точки минимума, поэтому целесообразно изменить направление движения. Подобная ситуация изображена на рис. 11.7, где X* - точка минимума, а шаг в точку Xi+i оказался неудачным. Схема описанного алгоритма представлена на рис. 11.8. Здесь а - величина пробного шага; % - случайный вектор, равномерно распределенный на поверхности п-мерной сферы единичного радиуса; параметр р рекомендуется задавать равным 0,5. Алгоритм 4. Алгоритм основан на выполнении последовательности преобразований растяжения-сжатия и преобразований вращения для такого преобразования системы координат, при котором матрица вторых производных (матрица Гессе) приближается к единичной, а направления поиска становятся сопряженными. В отличие от предыдущих, этот алгоритм использует квадратичную интерполяцию, поэтому его нельзя использовать при диалоговой оптимизации. Начало s=x+s; тончен 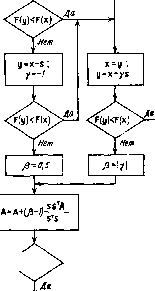 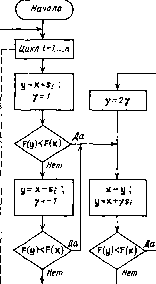
Рис. 11.5 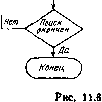  [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [ 87 ] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] 0.0128 |
||||||||||||||||||||||||||||||||||||||||||||