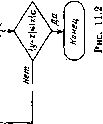
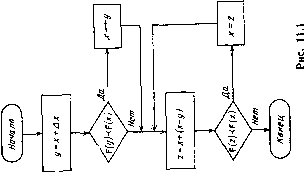
(лучше), чем в точке у, а F(x)j< F(y) означает, что значение критерия в точке X не хуже, чем в точке у.

Обычно оптимизационные задачи, возникающие при проектировании, являются не только многокритериальными, но и многоэкстремальными, т. е. целевая функция имеет несколько локальных минимумов, один из которых совпадает с глобальным. Методы решения многоэкстремальных задач, так или иначе основанные на планомерном просмотре всей допустимой области пространства параметров, являются весьма трудоемкими и требуют больших затрат машинного времени. По-видимому, ни один общий метод не позволит существенно сократить вычислительные затраты, поскольку уменьшение количества испытаний связано с риском пропустить область глобального минимума. В то же время различные приемы часто позволяют достаточно быстро отыскать точку, находящуюся в области притяжения глобального минимума. К таким приемам относится предварительное исследование упрощенной модели. Упрощение может заключаться в линеаризации всех нелинейных характеристик, тогда можно воспользоваться хорошо развитыми частотными или корневыми методами для определения начальных значений оптимизируемых параметров по заданным требованиям. Переход к полной модели (введение нели-нейностей) приводит к смещению точки минимума и изменению значений критериев, однако можно надеяться, что полученная точка является хорошим начальным приближением и находится в зоне притяжения глобального минимума.

11.2. ОДНОМЕРНЫЙ ПОИСК

Рассмотрим алгоритмы поиска при одном оптимизируемом параметре («=1). Эти алгоритмы используются также в многомерном поиске при минимизации вдоль выбранного направления. Задача нахождения точки минимума функции одной переменной решается в два этапа: определение интервала, содержащего точку минимума (интервала неопределенности) и последовательное сокращение интервала неопределенности до заданного размера. При многокритериальной оптимизации под точкой минимума понимается наилучшая точка.

Нахождение интервала неопределенности сводится к отысканию трех точек х, у, z, таких, что точка х расположена между у и Z и F (х) (у), F {х) ;± {)- Для этого выполняется серия возрастающих шагов до тех пор, пока точка минимума не окажется внутри интервала. Схема алгоритма приведена на рис. П.1. Входными данными являются начальная точка х и начальное приращение Ах. В результате работы алгоритма получаем три точки х, у, Z, такие, что х находится посередине между г/ и z и F(a:)j< F(i/), F(x)< F{z).

Для сокращения интервала неопределенности воспользуемся алгоритмом деления шага пополам (рис. 11.2). В результате работы этого алгоритма получаем точку минимума х, найденную с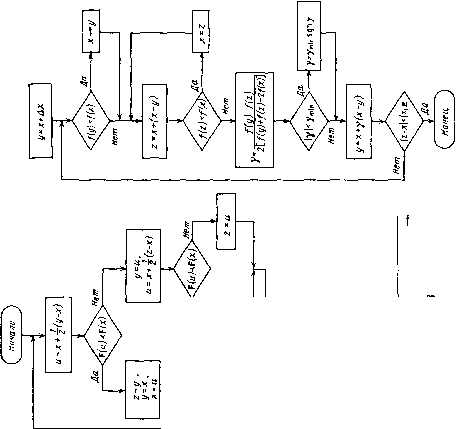

относительной ошибкой, не превышающей заданного значения е. Длина интервала неопределенности в данном алгоритме уменьшается в 2 раза после одного удачного испытания или после двух испытаний, первое из которых было неудачным. Если вероятность удачного испытания равна 0,5, то в среднем после каждых трех испытаний длина интервала неопределенности уменьшается в 4 раза.

Если целевая функция скалярная и достаточно гладкая, то для определения новой точки поиска имеет смысл воспользоваться квадратичной интерполяцией. По трем равноотстоящим точкам у, X, Z новая точка определяется из выражения

и=х+у{х-у),

[/(У)-/(г)] 2[/(/)4-/(г)-2/(х)]"

Схема алгоритма поиска с квадратичной интерполяцией приведена на рис. 11.3. В программной реализации алгоритма параметр Ymin выбран равным 0,02.

11.3. МНОГОМЕРНЫЙ ПОИСК

Рассмотрим новые алгоритмы поисковой оптимизации, три из них могут быть использованы при диалоговой оптимизации по векторному критерию.

Алгоритм 1. (Случайный поиск с адаптацией распределения пробных точек.) Приращение для пробного шага на j-м этапе этого алгоритма выбирается равным 8, = А,,-, где А,- - (пХл)-матрица; \i - случайный вектор, равномерно распределенный на поверхности л-мерной сферы единичного радиуса. Матрица Ai преобразует л-мерную сферу в л-мерный эллипсоид, на поверхности которого распределены пробные случайные точки.

В простейших алгоритмах этого типа Ai = ajl, где I - единичная матрица, а размер пробного шага Яг изменяется (адаптируется) в процессе поиска [69]. Их недостаток - низкая эффективность при минимизации овражных функций, поскольку пробные точки расположены на поверхности сферы и все направления поиска равновероятны. Для повышения эффективности поиска в этом случае следует повысить вероятность выбора наиболее благоприятных направлений, расположив, например, пробные случайные точки на поверхности эллипсоида, определенным образом ориентированного в пространстве параметров. В предлагаемом алгоритме пробные точки расположены на поверхности эллипсоида, определяемого матрицей А. В процессе поиска матрица А изменяется таким образом, что эллипсоид растягивается в удачных и сжимается в неудачных направлениях, благодаря чему он ориентируется в направлении оврага функции качества.

Опишем один этап поиска. Из текущей точки поиска Xj делаем пробный шаг, равный Si = \i%i. Если он оказался неудачным, делаем новый пробный шаг в противоположном направлении. Если