Рис. 9.9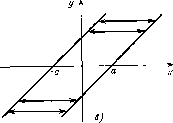

характеристиками. Однако наличие в системе неоднозначных и разрывных характеристик может вызвать серьезные трудности и привести к заметному снижению эффективности моделирования. Поэтому имеет смысл разработать для таких блоков специальные расчетные модели, ориентированные на использование совместно с численными методами интегрирования. В настоящем параграфе предложены расчетные модели некоторых наиболее типичных неоднозначных и разрывных характеристик.

В качестве моментов дискретизации при построении расчетных формул будем использовать моменты вычисления правых частей. Так, при использовании двухстадийного метода Рунге - Кутта на каждый шаг интегрирования приходится два момента дискретизации.

Рассмотренные здесь неоднозначные характеристики приведены на рис. 9.9. Определим выход неоднозначного блока в некоторый момент дискретизации, как функцию от его входа в тот же момент и выхода в предыдущий момент: уг = 1{щ, г/,-1). Тогда расчетные формулы для неоднозначных блоков будут следующие:

двухпозиционное реле (рис. 9.9,а)

У1 =

bsgn щ, \щ\> а,

трехпозиционное реле (рис. 9.9,6)

О, «,!<а.

csgnwj, «i>

нелинейность типа «люфт» (рис. 9.9,в)

«;-а, yi-i<Ui-a, щ + а, (/;-!> щ + а,

У1 =

Особые трудности возникают при цифровом моделировании разрывных характеристик, включенных в контур обратной связи 71инамического блока. Здесь приведены модели, обычно используемые при аналоговом моделировании нагрузки с сухим трением (рис. 9.10,а) и динамического блока с упором (рис. 9.11,а). Попытки использовать эти модели при цифровом моделировании часто приводят к неудачам, поскольку при совпадении выходного сигнала с точкой разрыва характеристики возникает скользящий режим, в результате шаг интегрирования начинает дробиться и решение практически останавливается. Для эффективного моделирования этих характеристик следует использовать логические условия, в зависимости от которых формируется выходной сигнал.

Рассмотрим влияние на динамическую нагрузку сухого трения (рис. 9.10,а). Особенностью этой характеристики является то, что если выходной сигнал становится нулевым, а входной не превышает по модулю момент трения, то выход остается равным нулю. Физически входом такого блока является сила, а выходом - скорость. При цифровом моделировании могут возникнуть три ситуации.

с Начало

1Е

интеграрования

Ml-г

ti-t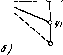

Рис. 9.10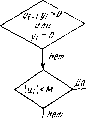

(Номец J

Рис. 9.11

Начало 1

Шаг интегрирования У /* ha.

1. Выходной сигнал не изменяет знак на интервале {ti-i, ti), тогда момент трения остается постоянным на этом интервале и для расчета очередного значения Уг используется обычный шаг (стадия) интегрирования.

2. Выходной сигнал изменяет знак на интервале {ti-u ti), а входной сигнал превышает по модулю момент трения (рис. 9.10,6). В момент времени t* переменная Z изменяется скачком на вели-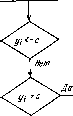

Коней,

чину 2М и выходная переменная терпит разрыв производной. При моделировании следует определить момент времени затем произвести пересчет на интервале {t*, /,+1) с учетом изменения знака момента трения.

3. Выходной сигнал изменяет знак на интервале {ti-x, ti), а входной сигнал не превышает по модулю момент трения. Тогда следует принять г/г = 0.

Алгоритм моделирования нагрузки с сухим трением на одном шаге дискретизации представлен на рис. 9.10,6. Для определенности здесь использован неявный метод Эйлера, однако может быть применен и любой другой метод интегрирования.

При моделировании динамического блока с упором (рис. 9.11,а) следует фиксировать значение выходной переменной в моменты, когда она пытается выйти за ограничения. Алгоритм моделирования динамического блока с упором на одном шаге дискретизации представлен на рис. 9.11,6.