Zi+i = Zi + hyi+u

Vi+i = Ui+i-KXi+l-Zi+u

Составление уравнений для приращений легко формализовать, если перейти от структурной схемы к схеме замещения. Дискретные модели замещения типовых блоков представлены в табл. 9.2, Здесь а - параметр метода интегрирования (для неявного метода Эйлера а=1, для метода второго порядка а=1-"К2/2), величины «, Ар в моделях замещения динамических блоков определяются через переменные, рассчитанные в момент ti. Схема замещения для схемы на рис. 9.7,а представлена на рис. 9.7,6, соответствует уравнениям (9.25).

Составленные таким образом уравнения для приращений выходных переменных могут быть представлены в виде

= 11 atjA yj + b, i = 1, ... , fe ; (9.26)

Аг/= S aijAyi+bi,i = k+\, ... ,in. (9.27)

Для приведения уравнений к такому виду следует выделить определяющие переменные уи yk, а все остальные переменные упорядочить определенным образом. Алгоритм выполнения этих действий будет описан ниже.

Матрица коэффициентов уравнений (9.26), (9.27) сильно разрежена и имеет обычно от одного до трех ненулевых элементов в каждой строке.

По уравнениям (9.26), (9.27) составим уравнения относительно приращений определяющих переменных

Аг/, = 2 А (/ + d„ г = 1, ... , fe. (9.28)

Для этого будем последовательно исключать неизвестные Аут, Дг/т-1, Аг/ft+i - в указанном порядке из уравнений (9.26), подставляя соответствующие выражения из (9.27) в (9.26). В процессе исключения используются только операции умножения и сложения, что гарантирует численную устойчивость. Последовательность действий может быть определена заранее и закодирована в виде соответствующих команд, в которых учитываются действия только с ненулевыми элементами.

Полученные уравнения (9.28) имеют, как правило, матрицу коэффициентов с небольшим числом нулевых элементов. Решение этих уравнений можно выполнить обычным методом исключения Гаусса. Поскольку число определяющих неизвестных значительно меньше общего числа блоков структурной схемы, решение этих уравнений не влияет существенно на общие вычислительные затраты.

Решая уравнения (9.28), находим приращения выходных сигналов определяющих блоков. Зная выходные сигналы определяю-

Бяои

Модель замеш,емая

и -» Л

и,

Uz

Ли,-

df(u,.U2) dfiupUz)

nr--;- Яр- -;-

ди, dU2

W(p)

щих блоков, по прямой схеме вычислений находим выходные сигналы всех остальных. При этом блоки, описываемые передаточными функциями, рассчитываются неявным методом по формулам § 9.3.

Для реализации предложенного здесь метода необходимо из всех блоков структурной схемы выбрать определяющие. Выбор определяющих блоков неоднозначен, однако для обеспечения эффективности метода необходимо, чтобы их число было минимальным. Алгоритм выделения минимального числа определяющих блоков рассмотрим на примере структурной схемы на рис. 9.8,а. Представим эту схему в виде ориентированного графа (рис. 9.8,6).

Алгоритм заключается в последовательном исключении вершин графа. Сначала исключаются вершины, соответствующие статическим блокам (на рис. 9.8,6 обозначены черными кружками), а затем вершины, соответствующие динамическим блокам. В качестве очередной исключаемой вершины выбирается вершина, имеющая

/ f J *

7 3 J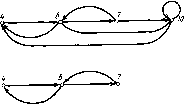

Рис. 9.8

наименьшее число входящих или выходящих дуг. Если после исключения очередной вершины образовалась петля, то вершина с петлей и инцидентными ей дугами удаляется из графа, а соответствующая этой вершине переменная включается в список определяющих.

После выделения определяющих переменных необходимо определить порядок расчета блоков. В первую очередь рассчитываются определяющие блоки, остальные блоки - в таком порядке, что каждый из них рассчитывается лишь после того, как найдены все его входные сигналы. Выделение определяющих блоков для рассматриваемого примера проиллюстрировано на рис. 9.8,в. Определяющие блоки (6 и 10) рассчитываются в первую очередь. Порядок расчета остальных блоков следующий: 1, 2, 7, 8, 9, И, 12, 3, 4, 5.

9.5. РАСЧЕТНЫЕ МОДЕЛИ НЕОДНОЗНАЧНЫХ И РАЗРЫВНЫХ ХАРАКТЕРИСТИК

Моделирование системы, представленной в виде структурной схемы, обычно не вызывает затруднений, если ее блоки описываются передаточными функциями и непрерывными однозначными