представим эти уравнения в матричной форме

Cx-a„r/ + b„« = 0,

0 ... о о

1 ... о о

(9.16) (9.17)

где А =

о ... 1 о

С = [0 ... о 1].

расчет процессов по уравнениям (9.16), (9.17) может быть выполнен явным методом интегрирования, если ОпфО. тогда из (9.17) получаем {Cx + bnu)lan и, подставляя это выражение в (9.16), получаем систему уравнений в нормальной форме коши. если ап = 0, то система алгебраических уравнений, получаемых при дискретизации уравнений (9.16), (9.17) любым явным методом, является вырожденной, и расчет процессов может быть выполнен только с использованием неявного метода.

применив к уравнению (9.16) неявный метод эйлера, получим:

Xi+i=Xi + hAxi+i-liAyi+i + hBvii+i.

объединяя это уравнение с (9.17), получаем систему линейных алгебраических уравнений

-ЛА; ЛА 1 Гхг+1 1 Txi + hBUi+i

- С ; а„ J Ui+i J L К ut+i использование любого другого неявного метода приводит к аналогичной системе линейных алгебраических уравнений вида

Sz-v, (9.18)

матрица коэффициентов которой равна

I-«АА "-С

ah А

an J

- ]

- ah о -1

О а hug

0 ahoi

1 aha-i

где а - параметр метода. для решения полученной системы алгебраических уравнений представим матрицу А в виде произведения нижней и верхней треугольных матриц:

A=LU,

Здесь gi.....„+1 определяются по рекуррентным формулам:

gi = ahao, gk = ah{ak-i+gk-i) {k=2..... л), gn+i=n + a„.

Решение системы уравнений (9.18) сводится к последовательному решению двух систем:

Lz=v - прямой ход,

Uz = z - обратная подстановка.

Расчетные формулы имеют следующий вид: прямой ход

обратная подстановка

Zn+l = n+l/gn+l, Zn = n-gnZn+U

Zn-\ =Zn-l-gn-\Zn+\,

(9.19)

Zl=Zi-lZ„+i.

(9.20)

Определитель матрицы A равен и не может быть равен нулю, если среди корней знаменателя передаточной функции f9.14) нет положительных. Таким образом, во всех имеющих практическое значение случаях система уравнений (9.18) невырождена, и расчет процессов может быть выполнен неявным методом.

Выведем теперь расчетные формулы, используя неявный метод второго порядка из табл. 9.1 к уравнениям (9.16), (9.17):

bn «1+1

Здесь а= 1-1/272.

Система алгебраических уравнений

(9.21)

(9.22)

может быть получена из уравнений (9.16), (9.17) путем формальной замены оператора дифференцирования на число l/(a/i) и по-

следующего умножения (9.16) на ah. Следовательно, решением системы уравнений (9.22) относительно у является г/ = Г(1/аЛ)ы,

где W{lfnh) - значение передаточной функции (9.14) при формальной замене оператора р на II{ah). Используя этот факт для решения уравнений (9.21), получаем: yi+a=W{lhh)Ui+a+Agu

yi+i = W{l[ah)Ui+i+Ag2. (9.23)

Здесь Л1, А2 находятся из уравнений

l+a + V2{Xi -1-а-Xj)

Начало

~~г~

Цикл k=Z.....п :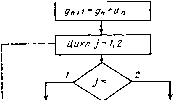

y(y*x„)/g„tr

ii/A-y? k=r,...,n: JCkXk-gy

no формулам, аналогичным (9.19), (9.20) для решения системы (9.18).

Алгоритм одного шага неявного метода Рунге - Кутта второго порядка для расчета процесса по заданной передаточной функции и заданному входному воздействию представлен на рис. 9.5. Входными данными алгоритма являются коэффициенты передаточной функции, шаг интегрирования и значения переменных состояния в момент времени t, выходными данными - значения переменных состояния и выходной переменной в момент t-\-h. (Алгоритм реализован в приведенной ниже подпрограмме PROC.)

Из уравнений (9.23) может быть получена дискретная модель замещения передаточной функции при расчете неявным методом, представленная на рис. 9.6. Подобные модели замещения будут в дальнейшем использованы при расчете процессов по структурной схеме.

Для мйогомерной системы, имеющей несколько входов и несколько выходов, передаточная функция в