реходный процесс наблюдения имеет колебательный характер и продолжается длительное время.

Зависимости, характеризующие уровень случайных средиеквадратических ошибок наблюдения, приведены на рис. 8.10 (непрерывными линиями показаны ошибки а - Уд (рассчитанные по (8.136)), соответствующие возмущенному режиму, а ошибки av = Vdvv I соответствующие невозмущенному режиму, - штриховыми линиями. Эти зависимости получены интегрированием (8.135). Все расчеты соответствуют oii==0,01.

Приведенные результаты математического моделирования свидетельствуют о целесообразности применения различных алгоритмов наблюдения в невозмущенном и возмущенном режимах.

ГЛАВА 9

МОДЕЛИРОВАНИЕ СИСТЕМ ВО ВРЕМЕНИ

Рассматриваются алгоритмы расчета процессов в автоматических системах при произвольных входных воздействиях. Математическая модель системы задана в виде уравиеннй состояния, матрицы передаточных функций, структурной схемы. Приведенные алгоритмы основаны на численных методах интегрирования дифференциальных уравиенин и учитывают специфику представления математических моделей.

•9.1. ЧИСЛЕННОЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИИ

Моделирование автоматических систем осуществляется путем численного решения их уравнений. Математическую основу алгоритмов моделирования непрерывных систем составляют численные методы интегрирования обыкновенных дифференциальных уравнений (ОДУ).

Численные методы интегрирования рассмотрим на примере ;автономной системы ОДУ, представленной в нормальной форме

x=f(x), х(о)=Хо. (9.1)

Здесь хо - вектор переменных состояния размерности п. Если система уравнений не является автономной и представлена в виде

x=F(x, t), (9.2)

«е нетрудно привести к виду (9.1), включив в состав переменных состояния переменную Xn+i = t и добавив к системе уравнений (9.2) уравнение x„+i=l.

Под численным интегрированием системы ОДУ будем понимать получение последовательности векторов х,, аппроксимиру-

ющих истинное решение на сетке ti = to-\- 2 hj, где hj - j-н шаг

интегрирования. Шаг интегрирования обычно выбирается, исходя из требуемой точности численного решения. Ошибка численного 216

решения состоит из двух составляющих: методической и вычислительной. Методическая составляющая ошибки, обусловленная неточностью метода, уменьшается с уменьшением шага интегрирования. Справедлива асимптотическая оценка методической ошибки при h~0 в виде ем=ск>, где k - порядок метода; с - некоторая константа. Вычислительная составляющая ошибки, обусловленная неточностью вычислений, возрастает при уменьшении шага интегрирования. Типичная зависимость результирующей ошибки е от шага интегрирования показана на рис. 9.1. Возможен случай,, когда значение етш больше допустимого. Тогда никакой шаг не обеспечит требуемую точность и для решения данной задачи следует использовать другой метод, обеспечивающий меньшее значение emin.

Одним из факторов, ограничивающих шаг интегрирования, является устойчивость численного метода. При численном интегрировании дифференциальные уравнения заменяются разностными. Решение разностных уравнений может оказаться неустойчивым, хотя соответствующие дифференциальные уравнения были устойчивыми. Неустойчивость проявляется как катастрофический рост ошибки численного решения при увеличении шага интегрирования. Такая ситуация изображена на рис. 9.1 при h~hmax-

Рассмотрим проблему устойчивости численного решения на примере системы линейных ОДУ

х=Ах, х(о)=Хо. (9.3)

Пусть система (9.3) устойчива, т. е. все собственные значения матрицы А имеют отрицательные действительные части. Применяя к системе (9.3) одношаговый метод интегрирования с постоянным шагом, получаем

Xi=[R{hA)yxo. (9.4)

Для явного метода Рунге - Кутта порядка k имеем 7?(/гА) = 1---\-hA-\- ... -\-{hA)/kl. Численное решение (9.4) является устойчивым, если вьшолняются неравенства

\R{h.Xi)\<:l, п, (9.5)

где .j-собственные значения матрицы А. Функция R{hX) комплексной переменной hk называется функцией роста одношагово-го метода [89], а неравенства (9.5) определяют область устойчивости метода в плоскости hX. На рис. 9.2 приведены области устойчивости явных методов Рунге-Кутта. Шаг интегрирования следует выбирать таким, чтобы все значения hXj (/=1,..., п) попали в область устойчивости.

Предположим, что все собственные значения матрицы А действительны и отрицательны. Тогда шаг интегрирования выбирается, исходя из наибольшего по модулю собственного значения. Однако решение системы ОДУ определяется в основном небольшими по модулю собственными значениями. При большом разбросе собственных значений приходится выбирать очень малый шаг интегрирования, хотя само решение изменяется медленно.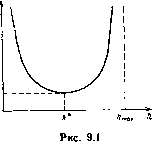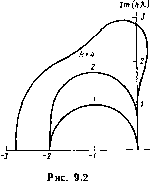

Проиллюстрируем это на примере системы, схема которой приведена на рис. 9.3. Характеристический полином этой системы равен p-j-lOp-j-lO", корни этого полинома XiXl, ijlO". Выход-,ной сигнал выражается формулой y{t)l-l,0001e~-fO,0001e~". Решение практически определяется составляющей е~, другая составляющая мала и быстро затухает. Несмотря на это при интегрировании явным методом Рунге - Кутта шаг следует выбирать порядка 10-" на всем интервале интегрирования. Интегрирование <; малым шагом приводит к увеличению времени счета и вычислительной составляющей ошибки.

В реальных системах разброс собственных значений может •оказаться таким большим, что использование обычных, явных методов практически не позволяет получить решение за приемлемое время и с заданной точностью.

Мы столкнулись с проблемой решения жестких систем ОДУ. Так называют системы, при численном решении которых традиционными методами приходится использовать очень малый шаг интегрирования, хотя искомое решение изменяется достаточно медленно. (Более полное определение жестких систем и исследование их свойств приведено в работе [68].) Практика показала, что явление жесткости в реальных сложных системах скорее прави-.ло, чем исключение. Это способствовало развитию методов интегрирования жестких систем [68, 78, 91, 92]. К таким методам следует отнести прежде всего неявные методы интегрирования. Простейшим из них является неявный метод Эйлера:

Xi+i=x,+M(xi+i). (9.6)

При реализации неявного метода Эйлера необходимо на каждом шаге интегрирования решать систему нелинейных алгебраических уравнений (9.6). Это яв-

ляется своеобразной платой за возможность решать жесткие системы. Применяя неявный метод Эйлера к системе (9.3), получаем