
 |
|
Главная страница Программы проектирования [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [ 70 ] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] 2. Интегрирование уравнений чувствительности (8.122). 3. Вычисление 6К<> согласно (8.127) и (8.128). При joo К<)-К, при этом имеет место квадратичная скорость сходимости. Отметим существенное обстоятельство, которое необходимо-учитывать при построении практических алгоритмов. Сходимость последовательности К<*, К<\... обеспечивается, если значение-КС достаточно близко к К. Выбор подходящего К" представляет собой самостоятельную задачу, поэтому численную процедуру определения параметров алгоритма наблюдения желательно строить так, чтобы ее применение не было связано с необходимостьк> специального вычисления К". Процедура, отвечающая этому условию, основана на минимизации функционала /(6К<) для последовательно увеличивающихся интервалов времени [о, to-\-bt], 6i<62,..., причем to-\-6ti< <ti. Эта процедура состоит в следующем. На первом интервале [о, o--6i] начальное значение матрицы искомых параметров принимается равным нулю К< = 0, а значение выбирается таким, чтобы определитель матрицы Ф(К<°)) = Ф(0) при 0+61 существенно отличался от нуля. Практически 61 оказывается приемлемой, если А= (50 ... 70)/г, где h - шаг интегрирования уравнений. Допустимое значение может определяться алгоритмически в процессе интегрирования соответствующих уравнений. При выбранном 8ti осуществляется последовательное вычисление К> в результате выполнения операций 1-3. При этом верхний предел интегрирования в (8.128) принимается равным to-\-bti. Пусть при /=71 какая-либо подходящая норма IIК-К<"<е, что означает достижение заданной точности приближения. Индекс 71 означает, что К соответствует первому интервалу (р=1). Задавая для второго интервала [о,. значение К<> = К< и выполняя операции 1-3, найдем K<v=)j при котором II К(г)-К("<е. Величина 62 может быть принята, например, равной 26i. Продолжением этого процесса для интервалов fo, to-\-bt] (р = 3, 4,...) обеспечивается решение исходной задачи минимизации /(К). Рассмотренный алгоритм обладает определенной компактностью и легко реализуется в ЭВМ. Построением процедуры вычисления параметров Kvh исчерпывается задача параметрического синтеза алгоритма наблюдения в возмущенном режиме. . Рассмотрим теперь невозмущенный режим наблюдения, характеризуемый незначительными динамическими составляющими ошибки по сравнению со случайными составляющими. Параметры Куц (О для возмущенного режима найдем из условия Q( K)=M[x(OBx(0]=min, где В - любая неотрицательно-определенная матрица, а x{t) - центрированная случайная составляющая оценки, определяемая дифференциальным уравнением (8.116). Значения параметров, при которых достигается минимальное значение, будем называть оптимальными (для невозмущенного режима) и обозначать Ку,ц (0=w (0. отмечая символом а тот факт, что при К(0 = КЧО имеет место минимум средиеквадратических ошибок (oia2 On)=o{t). Можно видеть, что определение К") составляет содержание задачи Калмана. Поэтому можно записать искомое решение в рассматриваемом случае: КС) (О = D (г) Н1(0 N-1 (0. b (О = F. (О D (О + D (О Fl(0- -D (t) W it) N- (0 H(t)D (t). (8.129) X ic о о Здесь D(0 = M[x(Ox()] - корреляционная матрица оценок, а матрицы H;(0 = [H, X) F; (0 = [F.( х)]-. Таким образом, задача наблюдения нелинейной динамической системы в рассмотренной постановке решается с помощью алгоритма, основу которого составляет уравнение (8.114). При этом параметры Кц (t) должны выбираться различными для возмущенного и невозмущенного режимов наблюдения. Для распознавания режимов наблюдения можно использовать приемы, аналогичные рассмотренным в § 8.4. Пример. Особенности процесса наблюдения в возмущенном и невозмущеи-«ом режимах проиллюстрируем на примере системы x(/)=F(;, X), х=(х, Xi), x{t) F(x) = p., u)>0, (8.130) описывающей движение инерционной массы, укрепленной на жесткой пружине. Восстанавливающая сила пружины изменяется нелинейно в зависимости от отклонения массы от положения равновесия. Пусть можно измерить координату Xl, так что y(/) = Hx(;)-f(/), Н=[! 0]. В соответствии с (8.114) алгоритм «аблюдения имеет вид =F((,x)-l-K(0 iy(0 -Нх(0], KHt) = [Kn(t)K2i{t)]. Для возмущенного режима выберем К(0=К таким, чтобы для каждого t>ta линейная система " = [F;c ( X) ~ К (О Н] бх (О, (8.131) F,(/, х) = Зцх2 (0-102 1 аналогичная (8.115), совпадала с эталонной системой П1(0=П2(0=-РгтЛО-Р22Т12(0. Р2\, P22 = const. (8.132) Из сравнения (8.131) и (8.132) имеем Яи(0=Р22, Я21(0=Р21-3nxi2(0-О). (8.133> Уравнение для центрированной случайной составляющей оценки: = [F ( Jt) - к (О н] X (О + к (О I (0. (8.134> Поэтому в соответствии с (8.129) оптимальные параметры для иевозмущеииогс режима определяются следующим образом: [11 (О КС) (0 = D(0 нт П7, D (/) = F . (/) D (/)-f D (О (/) - D (t) Нт HD (/) пГ/ • (8.135> Здесь Ли - интенсивность погрешности измерения На основании (8.134) можно записать уравнение для матрицы вторых моментов D(() при К(0 = К(0- Имеем D (О = S (О D (О + D {t) ST (/) - К (О К (О "11 S (О = (/, X) - К (О Н. (8.136> Перейдем к обсуждению результатов математического моделирования процесса наблюдения рассматриваемой системы. На рис. 8.9 непрерывными линиями показаны математические ожидания ошибок bxi, 6X2 оценивания координат xi, хг- Приведенные-зависимости соответствуют случаю, когда параметры алгоритма наблюдения вычисляются согласно (8.133). Расчеты выполнены при \i=\ и (0 = 2 с~. Кроме того, принято P2i = 12, р22 - 7, что обеспечивает затухание процессов в эталонной системе за 2 с. Как следует из рис. 8.9, продолжительность переходного процесса оценивания математических ожиданий координат изучаемого-движения около 2 с. Здесь же показаны математические ожидания ошибок наблюдения Axi, Ax2, рассчитанные также для возмущенного режима (штриховые линии). Однако в отличие от 61, 6x2 эти зависимости соответствуют случаю, когда параметры алгоритма Кп, к21 выбираются согласно (8.136); К(0 = = К("(0- В этом случае пе- 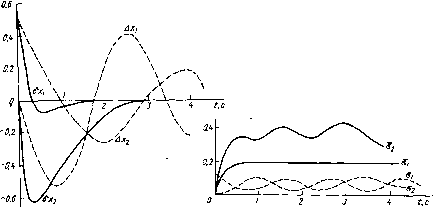 Рис. 8.9 Рис. 8.10 [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [ 70 ] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] 0.0127 |