Программа FILK

Назначение: моделирование уравнений движения объекта и фильтра Кал-

мана - Бьюси. Параметры:

вектор состояния системы, вектор управления, вектор случайных воздействий, матрица динамических параметров системы,

матрица коэффициентов усиления управляющих сигналов системы, матрица коэффициентов уоилеиня случайных воздействий, вектор выходных координат, вектор помех при измерениях, • матрица измерений, матрица коэффициентов усиления фильтра.

Используемые подпрограммы: RKE - решение системы обыкновенных дифференциальных уравнений методом Рунге -Кутта; ANORM - датчик случайных чисел с нормальным распределением, нулевым математическим ожиданием и единичной днспероией; PLOT - печать графиков.

А В С Y V Н К

Н,Й,н рад

200- 0,07 -

100 - 0,035 -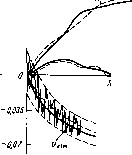

Рис. 8.3

В результате выполнения программы FILK получим реакцию системы на воздействие случайного вектора w (рис. 8.3). Моделироваине показывает, что даже в том случае, когда измеряется лишь одна координата б(0, фильтр дает точные оценки всех координат, максимальные ошибки не превышают 10%.

8.2. ОЦЕНИВАНИЕ ВСЕХ КООРДИНАТ СИСТЕМЫ ПРИ ОТСУТСТВИИ ШУМОВ НАБЛЮДЕНИЯ

В предыдущем разделе рассмотрена задача оценивания вектора состояния системы при наличии шумов в измерениях. Однако шумы в измерениях часто практически отсутствуют. Это приводит к тому, что корреляционная матрица ошибок наблюдения R(/) будет вырожденной. Обратная же матрица R~(0 входит как в дифференциальное уравнение Риккати (8.23), так и в вы-

ражение для матрицы коэффициентов усиления фильтра (8.19). Поэтому для наблюдений, не содержащих белых шумов, фильтр Калмана - Бьюси в его первоначальной форме уже неприменим. В этом случае одним из возможных способов восстановить вектор состояния является создание модели, в которой все ее переменные доступны измерению. Основные трудности этого способа состоят в том, что необходимо точно знать динамические параметры системы, при этом начальные условия в модели и системе должны совпадать. Кроме того, искажения входных сигналов, воздействующих на систему, не всегда могут быть введены в модель.

Другой способ основан на дифференцировании доступных измерению координат некоторое число раз и получении недостающих координат как линейных комбинаций производных. Однако и в этом случае ошибки неизбежны из-за отсутствия хороших дифференцирующих устройств и сильной чувствительности к шумам.

Ниже рассмотрим метод восстановления всех компонентов вектора состояния, который был развит Калманом в работе [34].

Пусть линейная наблюдаемая система описывается уравнениями

x{t)=\{t)x{t)+B{t)u{t), x{to)=Xo; (8.29)

y{t)=C{t)x(t), (8.30)

где X(О-«-мерный вектор состояния системы; и( --мерный вектор управления; у() -т-мерный вектор выходных координат; А(), В() и С() -матрицы размера пХп, пХг, тХп соответственно.

Если матрица C[t) не вырождена, то вектор состояния может быть легко найден из выражения

х(/)=С-1(0у(0- . (8.31)

В противном случае вектор состояния можно определить с помощью линейной наблюдаемой системы (фильтра), описываемой векторным дифференциальным уравнением

z(0 = D(0z(0-fE(0u(0-fF(0y(0. z(/o)=Zo. (8.32)

где z(0-«-мерный вектор состояния фильтра: D{t), £(/) и F(О-матрицы размера яХ«, «Хг, пХт соответственно. Для этой системы векторы u{t) и y{t) являются входными воздействиями. Предположим, что параметры фильтра можно подобрать такие, что

z{t)=lx{t), (8.33)

где Т - постоянная невырожденная матрица.

Определим условия, которым должны удовлетворять матрицы D(/), Е(/) и F(/) фильтра (8.32). Для этого умножим обе части уравнения (8.29) слева на матрицу Т, а равенство (8.33), продиф-

ференцировав по времени, подставим в уравнение (8.32). Тогда,

используя соотношение (8.30), получаем:

Тх (О ==ТА (t) x (О +ТВ (t) и (О, (8.34)

Tx(0 = D(OTx(0+F(OC(Ox(0 + E(Ou(0. (8.35)

Из равенств (8.34) и (8.35) следует

T\{t)-D{t)T=F(t)C{t); (8.36)

Е(0 = ТВ(0. (8.37)

Если матрицы А(/) и D{t) не имеют общих собственных значений, то при постоянных матрицах А (О, D(0. С (О и F{t) уравнение (8.36) будет иметь единственное решение относительно Т. Этот результат получен в [45].

Вычтем уравнение (8.34) из (8.32) с учетом равенств (8.36) и (8.37). В результате получим линейное однородное дифференциальное уравнение относительно переменной z(t)-Tx{t):

z-Tx=D(t)[z{t)-Tx(t)], (8.38)

которое имеет хорошо известное решение

z(t)-x{t) = Ф{t, /o)[z(o)-Tx(/o)]. (8.39)

где Ф {t, to) - фундаментальная матрица, удовлетворяющая уравнению

Ф(А о) = 0(ОФ(/, to), Ф{to, to) = l. (8.40)

Из уравнения (8.40) следует, что матрицу D(/) необходимо выбирать такой, чтобы действительные части ее собственных значений были строго отрицательными. Тогда переходный процесс, вызванный ошибкой установки начальных условий в наблюдаемой системе и фильтре, будет, как правило, быстро затухать, что позволит такой фильтр считать хорошим.

Для упрощения вычислений положим Т=1, где I - единичная матрица. Тогда из (8.36) и (8.37) получим

D(0 = A(0-F(OC(0; (8.41)

Е(0 = В(0. (8.42)

При этом уравнение фильтра примет вид

z(0 = [{t)-F{t)C(t)]z(t)+Щt)Vi(t)+F{t)C(t)x(t), (8.43)

который может быть построен в соответствии со структурной схемой на рис. 8.4. Это устройство оценки вектора состояния является фильтром Калмана - Бьюси с известным входным сигналом u{t). Коэффициент усиления фильтра F{t) следует подбирать так, чтобы фундаментальная матрица в (8.39) быстро убывала до нуля.

Недостаток рассмотренного метода состоит в том, что фильтр оценивает все переменные состояния, хотя некоторые из них (по крайней мере одна) уже наблюдаемы, а некоторые могут не представлять интереса [73].