Таблица 6.1

/ Исходные duMHbie А,В.Н.с=5 /

Алгоритм минимизацией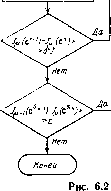

Считаем, что все три координаты х\, Хг, вектора состояния доступны для непосредственного измерения. Следовательно, в (6.7) матрица Н==1, поэтому закон управления (6.8) будет

и (X) = СХ (О = CxXi it) + С2Х2 (t) + С3Х3 (/).

Процесс поиска оптимальных параметров с*,, основанный на минимизации функционалов /ц, характеризуется данными табл. 6.1 для случая, когда в минимизируемом функционале принято

"1 О 0-

Р=1.

Процесс минимизации для каждого интервала Тц заканчивался при выполнении неравенства (6i-f622-1-бз)0,01. Первое значение 7i = 0,7 с, последующие значения Гц равны удвоенным значениям предыдущих. Общее число циклов оптимизации 12, что свидетельствует о высокой скорости сходимости вычислительного процесса.

Отметим, что точные значения оптимальных параметров равны с*1 =-1,04; с*2=-2,7; с*з=-3,25. Можно видеть, что найденные значения параметров закона управления практически совпадают с оптимальными.

Заметим, что интервал времени [О, Ti] следует назначать таким, чтобы определитель матрицы р(с, Ti) существенно отличался от нуля. Выбор последующих интервалов допускает определен-

ный произвол. Они могут быть приняты, например, равными Т = = Т -i + Ti/2 {ц = 2, 3, ...). На практике при назначении Ti можно руководствоваться следующими рекомендациями. Пусть динамические свойства синтезируемой системы таковы, что численное интегрирование соответствующих дифференциальных уравнений можно проводить с шагом Л. Тогда Ti целесообразно принять равным (50...70)Л.

В рассмотренном примере передаточная функция управляемого объекта имеет нулевой полюс тройной кратности. С такой же эффективностью приведенный алгоритм может быть использован для поиска оптимальных параметров управления и для неустойчивых объектов.

«.3. УПРАВЛЕНИЕ ВЫХОДОМ ОДНОМЕРНОЙ СИСТЕМЫ

Математическую модель управляемого движения принимаем в виде

= Ax(0 + bu(0. х(0) = х„;

ы(х) = сНх(0. y{t) = q x{t).

Используемые здесь обозначения соответствуют (6.1) и (6.8). Как и в предыдущей задаче, считаем, что число измеряемых коорди-«ат kn. Параметры Ci, Сг, .... закона управления будем определять из условия, что функционал (6.5) принимал минимальное значение на траекториях движения замкнутой системы (6.22) из точки Хо в начало координат.

В рассматриваемом случае параметры Cj необходимо определить из условия, чтобы выходная переменная y{t) системы удовлетворяла требованиям, которые обеспечивают минимум функционала (6.5). На этом основании рассматриваемую задачу называют задачей управления выходом системы. Покажем, что оптимальные параметры Ci, Сг..... Ch могут быть вычислены с помощью

алгоритма, «оторый построен в § 6.2 для решения задачи управ-.ления состоянием.

В соответствии с (6.22) квадрат выходной переменной опреде-.ляется так:

yHt)iqt)) = x-{t)qqrx{t).

С учетом этого выражения минимизируемый функционал (6.5) яринимает вид

J (и) = [[х- (О qq X (О -f Р (t)] dt. (6.23)

Сравнивая (5.22) и (6.23), замечаем, что оба функционала сов-шадают, если в (6.23) принять qq = V. Отсюда следует важный вывод: алгоритм определения оптимальных параметров закона управления состоянием системы справедлив и для задачи управ-

ления ее выходом. Таким образом, для оптимизации замкнутой системы (6.22) по минимуму (6.23) используются все расчетные соотношения § 6.2. В них необходимо принять V=qq.

6.4. УПРАВЛЕНИЕ МНОГОМЕРНОЙ СИСТЕМОЙ

Уравнения управляемого движения многомерной системы принимаем в виде

:Ax(0+Bu(0, х(0) = х„; 24)

y(0 = Qx(0.

Здесь U - т-мерный вектор управляющих функций; у - г-мерный вектор выходных переменных. Остальные обозначения соответствуют ранее введенным. Предполагается, что система (6.1) вполне управляема и наблюдаема. Опираясь на результаты § 6.3, изложим методику построения алгоритмических процедур решения классических задач аналитического конструирования для многомерного случая. Здесь также будем считать, что для вычисления управляющих функций щ, Um может использоваться ограниченный объем информации о состоянии управляемого объекта. Для модели (6.24) это означает, что матрица Q имеет размер г Хга, причем гп. В частном случае структура матрицы Q может быть такой, что она выделяет измеряемые координаты состояния. Тогда yj(i) будут совпадать с Xj(t), доступными для измерения.

УПРАВЛЕНИЕ СОСТОЯНИЕМ СИСТЕМЫ

На движениях системы (6.24) задан функционал

/(u) = j [xm)\x{t)+u4t)Tu(t)]dt, (6.25)

где V - неотрицательно-определенная и Г - положительно-определенная матрицы. В каждый момент времени известны выходные переменные yi(t), г/г (О- Требуется найти такие значения параметров [c,j] = C закона управления

u(x)=Cy(0=CQx(0, (6.26)

при которых реализуется минимум функционала (6.25).

При полной степени наблюдаемости, когда г = га, yi{t) =Xi{t), искомые параметры отыскиваются в результате решения матричного уравнения Риккати, которое вытекает из классической теории аналитического конструирования оптимальных регуляторов. При неполной степени наблюдаемости классическая теория решения не дает. Построим алгоритмическую процедуру вычисления оптимальных параметров с*,-, закона управления (6.26).

Как и для одномерных систем, нелинейную задачу минимизации функционала /(и)=/(С) по С необходимо свести к решению 134