приводит к оптимальному значению c* = limc*+. При этом

6=-P~{cS Г)v(c Т), v(c T)=lg{t, c)dt;

g(/, сО = т1(, c)Vti( сО + Рф(/, cOz(/, c»)c

R (/, = T]- cO V Tl (/, c») + рф if, C) r it. c»). (6.20)

В соответствии с принятыми обозначениями (6.8) здесь

ф(, c)=Wt, c)c+z{t, с«),

W{t, c) = Hri{i, с);z{t, с) == Нх( с). .(6.21)

Полученные соотношения позволяют построить алгоритм определения оптимальных значений параметров синтезируемой системы.

1. Интегрирование дифференциального уравнения замкнутой

системы

х( с«) = (A + bc«H)x(i, с»), х(0, с«) =Хо.

2. Интегрирование матричного дифференциального уравнения для функций чувствительности

т)( c«) = (A+bc«fH)T)(i, c»)+bx(i, с»)Н т)(0,с«)=0.

3. Интегрирование выражений

V(c t)=g(!t, с«), v(c 0)=0; Р(с«, i)=K(t, с), Р(с\ 0)=0,

где вектор-функция g и матрица R вычисляются по i(6.20), .(6.21).

4. Интегрирование выражения

u (cO = c« Hx (/, c; J (c 0) = 0.

5. Выполнить сравнение: если t-7<:0, продолжить интегрирование, перейти к п. 1; если t-ГО, окончить интегрирование, перейти к п. 6.

6. Вычислить новое приближение с*+=с«-Р-(с, T)y(c, Т).

7. Напечатать результаты, s, с«, /(с«, Т).....

8. Проверить признак окончания оптимизации: если /(С, Т) - -/(€«+, Г)>е, повторить цикл оптимизации, перейти к п. 9; если J{c\ Г)-/(с»+1, Т)е, счет окончен.

9. Восстановить начальные условия

х(0, с«)=хо, Ti(0, с«)=0, у(с\ 0)=0; Р(с», 0) =0, /(с», 0)=0.

10. Передать управление на п. 1 для повторения цикла оптимизации.

."i-fiq 129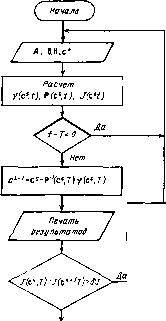

Восстанодить начальные условия

Конец

Схема алгоритма приведена на рис. 6.1. В одном цикле выполняются предписания 1 ... 4, в результате вычисляются все величины, необходимые для формирования линейного векторного уравнения относительно поправки 6 Интегрирование выполняется до момента времени t = T. После этого вычисляется очередное приближение с«+ согласно (6.19), печатаются результаты счета и проверяется признак окончания оптимизации. Если разность /(с«, 7)--/(€«+, Г) меньше некоторого заданного значения, характеризующего требуемую степень приближения /(с«)->-/(с*), то вычисления прекращаются. Если требуемая точность не достигнута, восстанавливаются начальные условия, и цикл оптимизации повторяется.

Данные о размерностях векторов и матриц, входящих в расчетные соотнощения алгоритма: А=(пХп), Ь=(пХ1), с=(йХ1), Н= (Хп); х=(пХ1), z=(feXl), л=(Хй), Р=(ЙХ); v=(Xl), (р=(ЛХ1), Ч=(АХй).

В представленном алгоритме процесс оптимизации заканчивается, если минимизируемый функционал /(с«) при очередном приближении практически остается постоянным. В качестве признака окончания оптимизаций можно использовать также неравенство 16«1Р<8с, где Ее - малая величина. В этом случае последовательные приближения прекращаются, если поправки 6« становятся малыми. Целесообразность использования того или иного признака (или обоих одновременно) может быть установлена в зависимости от особенностей конкретного объекта. Это выполняется в результате математического моделирования.

При построении алгоритма предполагалось, что управляемая система устойчива. В таком случае процесс оптимизации можно начинать при нулевом значении с = 0. Если собственное движение системы неустойчиво, то вычислительный процесс может оказаться расходящимся.

ОБЕСПЕЧЕНИЕ СХОДИМОСТИ ВЫЧИСЛИТЕЛЬНОГО ПРОЦЕССА

Выбор начальных приближений в нтерационных численных схемах всегда сопряжен с известными затруднениями. Здесь мы рассмотрим способ организации вычислительного процесса, при-

Рис. 6.1

менение которого позволяет провести оптимизацию проектируемой системы при начальном значении вектора искомых параметров €" = 0. Этот способ основан на последовательной минимизации функционалов

(и) = f*" (х- (О Vx (О + (0) dt, Т,<Т,<Т,<...,

на увеличивающихся интервалах [О, Гц] (х=1, 2, ...). В этом случае вычислительный процесс организуется следующим образом.

На первом интервале [О, Ti] в алгоритме оптимизации принимается c° = Q. При таких исходных данных отыскивается минимум Ji(u). Пусть при s = si для вектора 6* выполняется условие 6*11*<ес, что свидетельствует о достижении заданной степени приближения к экстремуму Ji{u). Обозначим через с« найденное значение вектора параметров, которое соответствует этому экстремуму. На следующем интервале [О, Гг] минимизация функционала /2(«) выполняется при начальном значении с° = ск Назначенная окрестность экстремума будет достигнута при некотором s = = S2; пусть ей соответствует вектор сЧ Он принимается в качестве начального {с° = с) на третьем интервале [О, Гз] минимизации функционала /з(") и т. д. Этот процесс последовательной минимизации продолжается до тех пор, пока верхний предел интегрирования станет равным Г. Нет необходимости доказывать, что последовательность С, с««, ... стремится к оптимальному значению с*.

В качестве признака окончания процесса оптимизации можно использовать неравенство 1/(сь)-/(с*- )1<е, где е - малая величина. Именно для такого признака на рис. 6.2 представлена схема организации вычислений. Алгоритм минимизации J, строится по схеме на рис. 6.1. При каждом интервале T осуществляется поиск такого вектора c, который соответствует заданной е-окрестности локального минимума интеграла /ц. После этого верхний предел интегрирования увеличивается на АГ, и цикл минимизации повторяется при новом начальном значении c = c. Такой процесс продолжается до тех пор, пока е не достигнет окрестности глобального минимума. Вычислительный процесс начинается при с"-О и некотором значении Гь задаваемом в массиве исходных данных. Верхний предел интегрирования Г в функционале J(u) определяется в алгоритме косвенно, с помощью признака окончания вычислений.

Чтобы показать эффективность изложенного приема обеспечения сходимости процесса параметрической оптимизации, приведем результаты математического моделирования.

Для уравнения (6.1) управляемой системы принимаем следующие значения:

5* 13!