ему многочлена с корнями, симметричными относительно мнимой оси, в виде явной функции от элементов весовых матриц Ф и F. Из этого выражения можно определить значения весовых коэффициентов по заданному спектру матрицы оптимальной системы. В случае диагональной матрицы Ф и единичной матрицы ¥ можно составить простую систему линейных уравнений относительно элементов фгг(=1. •••> «). если приравнять коэффициенты, расположенные слева и справа от знака равенства (5.46) при одинаковых степенях s.

Алгоритм нахождения весовых коэффициентов будет следующий.

1. Исходя из требований к переходному процессу оптимальной системы выбрать корни характеристического уравнения (5.40) аь 02,..., On, которые должны быть расположены в левой «-полуплоскости.

2. Рассчитать коэффициенты характеристического полинома обобщенной системы по формулам Ас-sl = (-1)"Д(s)A(-s),

A(s)= П (s-Oi); Д(-s)= П (-s-a,). i=i i= I

3. Рассчитать коэффициенты характеристического полинома

разомкнутой системы A(s) и произведения A(s)A(-s), раскрыв определители Д(5)Д(-s) = A-sl A-t-sI.

4. Вычислить полином правой части равенства (5.46), раскрыв определитель det[I + (A-t-sl)~X ХФ(А-sI)-iB4-Bt], где Ф - диагональная матрица с элементами фи, ф22, Фпп, а ¥ -единичная матрица.

5. Определить значения элементов весовой матрицы Ф, приравнивая коэффициенты при одинаковых степенях s в равенстве (5.46).

Если в результате расчета матрицы Ф окажется, что хотя бы один из ее элементов имеет отрицательное значение, то оптимальная система с заданным спектром собственных значений не может быть реализована, так как матрица Ф не будет отвечать условиям положительной полуопределенности.

Для систем высокого порядка (п4) предлагаемый алгоритм целесообразно реализовать на ЭВМ, используя систему аналитических вычислений ALCOR

а,в,(Х,,042,..., CLn

Определение элементов матрицы Ф

Решение ираднения

ka + ak-kbv

D=4-Bk Коней,

Рис. 5.7

[65]. В этом случае расчет коэффициентов передачи оптимального регулятора может быть выполнен по алгоритму, схема которого приведена на рис. 5.7.

Пример. Рассмотрим задачу об оптимальном управлении боковым движением самолета. Пусть это движение описывается системой дифференциальных уравнений вида (5.30), причем вектор состояния и вектор управления имеют вид

X-=[Xi Х2 Хз Xi X5] = [l> Ыу у (Ох Р]; U=[«i «2] = [бнбэ].

Здесь - угол курса, рад; у - угол крена, рад; р - угол скольжения, рад; Wx и (Оу - проекция вектора угловой скорости на связанные оси координат, рад/с; би - угол отклонения руля иаправления, рад; бэ - угол отклонения элеронов, рад.

Матрицы А и В равны

-0,098 О

-0,089 1

-0.63 0,16

0.9 -0.016 -2,3 О

Требуется рассчитать коэффициенты передачи оптимального автопилота, который бы обеспечивал в замкнутом состоянии следующие собственные значения: ai=-0,26; 02,3=-0,66±j 1,3; 04,5=-2,l±i 1,8.

Предположим, что весовые матрицы в квадратичном критерии качества (5.31) имеют вид

Ф=с11ае[фп О фзз О 0]; Y-diagLl 1].

Тогда задача сводится к вычислению весовых коэффициентов фп и фзз, при которых система управления в замкнутом состоянии будет иметь заданные характеристические числа.

Ниже приведена програйма ALCH, составленная по этому алгоритму.

Программа ALCH

Назначение: вычисление характеристического полинома )матрицы Ас по заданным собственным значениям. Параметры:

А - матрица параметров обобщенной системы Ас. D - характеристический полином матрицы Ас.

Ниже дан текст программы иа языке системы ALCOR. В результате работы программы получим

(Ас-sl=,(-1)5 П (s-ai)l(-S-ai)=s"+0,ls457;17s4

-f 132,39s<-t-255,2s»- 17,86.

Характеристический полином обобщенной системы, коэффициенты которого будут выражены через весовые коэффициенты фп и фзз, получим, используя программу ALCP.

V,Ji рад

D,ak- -

0.0 г -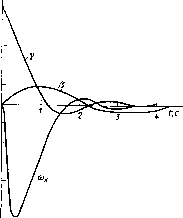

Программа ALCP

Назначение: вычисление характеристического полинома матрицы Ас в виде явной зависимости от весовых коэффициентов.

Параметры:

А - матрица динамических па- раметров системы размера пХ«.

В - матрица коэффициентов уси- -ди

леиия управляющих воЗДей-

ствий размера пХг, F - весовая матрица Ф, PSI - весовая матрица D - характеристический полином

матрицы Ас. (О,,рад/с

Ниже приводится текст программы, Ри g g

написанный на языке системы ALCOR. В результате работы программы получим

I Ас-I = s°+0,158+1(0,42фц+6,1 фзз-6,67) s«+ (-0,41 ф„+

+15,36фзз-6,49) s<+ (1,7ф, 1фзз-2,16ф„ -f 13,28фзз+0,О1) 5-

-О.ООббфпфзз-1,89ф,1.

Приравнивая коэффициенты двух характеристических уравнений при степенях и будем иметь

0,42ф11+6,1фзз=63,84; -0,41ф11+15,36фзз= 138,88.

Решив эту систему уравнений, получим ф11=115, фзз=9,5.

Подставим численные значения матриц Ф и Т в уравнение Риккати (S.36) и решим его. Затем по формуле (5.37) вычислим матрицу коэффициентов обратных связей оптимального автопилота:

Г-1,72 -0,89 0,95 0,32 -0,6 ~ [ 1,93 -0,07 -3 -1 0,87.

Процесс отработки самолетом начального рассогласования по углу крена у(0) = =0,05 рад с таким автопилотом показан на рис. 5.8.

Б.б. АНАЛИТИЧЕСКОЕ КОНСТРУИРОВАНИЕ ОПТИМАЛЬНЫХ РЕГУЛЯТОРОВ ПО КРИТЕРИЮ ОБОБЩЕННОЙ РАБОТЫ (А. А. КРАСОВСКИЙ)

В этом параграфе мы проведем алгоритмизацию процедуры аналитического конструирования, вытекающей из теории оптимизации по критерию обобщенной работы. Как и в других задачах, здесь представлена структура алгоритма, программа для ЭВМ и рассмотрен модельный пример. Вопросы алгоритмизации метода рассмотрены здесь для линейных моделей. Универсальные алго-