Т1араметры:

А - матрица динамических параметров системы,

В - матрица коэффициентов усилеиия управляющих воздействий,

D - матрица коэффициентов передачи обратных связей,

N - число координат состояния системы,

R - число управляющих сигналов,

ми - вычисленная матрица коэффициентов чувствительности размера гХя.

Используемые стандартные подпрограммы [53]: GMPRD - произведение двух матриц общего ввда, GMSUB - вычитание двух матриц общего вида.

Подпрограмма KORN

Назначение: вычисление корневых коэффициентов чувствительности.

Обращение: CALL KORN (А, В, D, N, -R, NU).

Параметры:

А - матрица динамических параметров системы,

В - матрица коэффициентов усиления управляющих воздействий,

D - матрица коэффициентов передачи обратных связей,

N - число координат состояния системы,

R - число управляющих сигналов,

NU - вычисленная матрица корневых коэффициентов чувствительности.

Используемые стандартные подпрограммы [53]: GMPRD - произведение двух матриц общего вида, GMSUB - вычитание двух матриц общего вида, EVGPD - вычисление коэффщиентов характеристического полинома и собственных значений действительной матрицы общего вида.

Пример. Рассмотрим задачу синтеза системы управления продольным движением самолета [51]. Пусть это движение описывается стационарной системой линейных дифференциальных уравнений вида (5.1), причем векторы состояния и управления имеют вид

x=[xi Xi Хз Xi Xs] = [V a & (Oz X Y]; u=[«i «2] = [бв бег].

Здесь V - путевая скорость полета, м/с; а - угол атаки, рад; # - угол тангажа, рад; (Ог - угловая скорость тангажа, рад/с; X - путь, м; Y - высота полета, м; бв - угол отклонения руля высоты, рад; бс.г - угол отклонения ручки сектора газа, рад.

Значения элементов матриц А и В равны

-0,26-10-2 0,87 -9,82 О О 0,2-10-Г

0,16-10-3 -0,58 О 1 О 0,3-10-»

0 О О 10 0 0,22-10-3 -0,497 О -0,75-10-1 0 0,15-10-»

1 О О ООО О -253,8 253,8 О 0 0

-0,Ф -0,26-10-1 О -0,157 О О 0,19 -0,8-10-* О 0,2.10-» О О Требования, предъявляемые техническим заданием, определяют следующие максимально допустимые отклонения переменных состояния: Almai=2 м/с, Датах =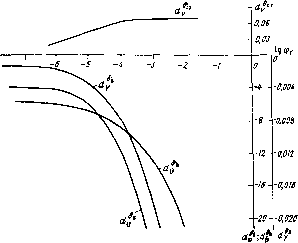

Рис. 5.5

=0,02 рад, Admai=0,01 рад, A(0zmai=0,01 рад/с, AX max~50 M, ЛУтах-20 M. Максимальные эначеиия отклонения руля высоты и ручки сектора газа соответственно равны Абв max-0,05 рад; Лбс.гтах=0,05 рад. Согласно выражениям (5.6), (5.7) вычиоти приближенные значения элементов весовых матриц критерия оптималыности (6j2):

©-diag[0.2-10-» I 10 10 0.3-10-* 0,2-10-5], y=diag[l 1].

Анализ переходных процессов, полученных прн отработке начального рас-согласовавия по таягажу д(0)=0,05 рад показывает, что первоначально выбранные значения элементов весовых матриц Ф и V яе удовлетворяют требованиям, предъявляемым к системе, так как обратные связи по углу та1игажа и угловой скорости тангажа, идущие на руль высоты, оказались весьма глубокими, а связь по высоте слабой.

С помощью программы MAD построим зависимости коэффициентов передачи оптимального регулятора и траектории собственных значений матрицы Ао при изменении фг. Некоторые из полученных зависимостей коэффициентов передачи приведены иа рнс. 5.5, а вдд корневого годографа для рассматриваемого случая - иа рнс. 5.6. Используя эти графики, можно уточнить значения веоов&х коэффициентов:

® = diag[0,2.10- 1 1 1 0,3-10-е 10-*],

Рис. 5.6 4=diag[il 1].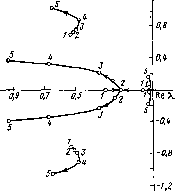

подпрогтажа domin/

suefoutine: H)MIN(a,B,d,N,r,MU) integer r

real m(2.6),ma,)

dimension M6,6).bl6,2) ,Ы2,6) ,Ш6,6) .Wi<.6,6\.WH2,6)

CMX GHPRD(B,d,BD,n,r,N)

call ghsub(a,BD,aa,N,n)

га.та=*.1е-в7

do i l=1,R

do 6 >1,N

atmx=».lE-12

do 4 1=1,N

if((ABS(B(i,L)»n(l,j))).gt.i]eLTA) go to 1

f«(i)=».e

go to 3

1 if((abs(aa(i,j))).gt.i£lta) go TQ 2 hn(i)=»,le+»7

60 to 3

2 hn(i)=abs(B(i,L)»d(l,j))/abs(aa(i,j))

3 ircmdv.gt.wfax) 60 to 4 goto 5

5 NU(L,J)=«»X

6 CONTINUE RETURN

С

С подпротажа korn

sueroutime kqrn(a,b,D,N,R,t«j) integer R

real nu(2,(l»,Itt(7),IMe(7),nn(6)

dikension M6,6>,b(6,2) ,Ы2,6),Ш6,6) ,aa»(6,6), » bd(6,6),Dn(2,6),C(7),re(7),bb(7),

» c»(7),REe(7),bbe(7),»<(2,(ll)

call GNFia>(b,n,bd,N,R,N)

cm.L gmsub(a,bd,aa,n,N)

сл.е egcpd(aa,C,re,Itt,bb,N,l,ier)

do 1 1=1,R

do 1 3=1,N

iin(I,j)=I»(I,j)

do 6 1=1 ,R

do 6 J=1,n

smax=e.le-12

d(I,j)=«.

call g«prd(b,d,bd,n,R,n)

call ghst№(a,bd,aae,N,n)

call evcpd(aae,c»,re»,iw»rBB0,n,l,ier)

do 3 K=1,N

IFCREeCK)) 2,4,4

nn(K)=swtt((re(K)-ftE»(K))»»2+(im(K)-im9(K))»»2) »/sort(re(K)»»2+itt(K)»»2) if(NN(K).gt.smax) smax=nn(K) nu(I,J)=smax go to 5 nu(i,J)=1.E+12 n(I,j)=dn(i,J) continue

print 7,((nu(i,J),J=1,n),i=1,r) formatdx, )*>= ,6e12.4) return end