Способ 2. Основан на учете влияния изменения обратных связей на положение корней характеристического уравнения системы на комплексной плоскости.

Корневым коэффициентом чувствительности стационарной системы к изменению параметров обратных связей будем называть число

Is- J /

vj. = niax---, (5.18)

k ISftI

где Sk - корни характеристического уравнения оптимальной системы; Ski - корни характеристического уравнения системы, полученной из оптимальной при обрыве обратной связи с коэффициентом dij. Корни будем нумеровать в порядке возрастания их действительной части. Величина корневого коэффициента чувствительности Vjj характеризует, несколько отбрасываемая обратная связь смещает корни характеристического многочлена системы.

Алгоритм определения чувствительности системы к параметрам обратных связей по второму способу следующий:

1. Вычислить матрицу параметров обратных связей по формуле (5.3).

2. Вычислить матрицу Ао и найти ее собственные значения.

3. Найти матрицу А*о параметров систем, полученных из оптимальной при обрыве обратной связи с коэффициентом dj,, и их собственные значения.

4. Вычислить значения корневых коэффициетнов чувствительности по формуле (5.18) и составить из них матрицу чувствительности N = [vij].

Примечание. Если при отбрасывании какой-либо обратной связи появляются характеристические числа матрицы А*о, расположенные в правой полуплоскости, то коэффициент ,vij для этой связи считаем равным бесконечности.

5. Отбросить обратные связи с коэффициентом \ц<ь, считая их несущественными.

Вычисление матрицы коэффициентов чувствительности системы к параметрам обратных связей N целесообразно проводить на ЭВМ с еомощью разработанной подпрограммы KORN, схема алгоритма коротой приведена на рис. 5.4.

После отбрасывания несущественных обратных связей необходимо оценить приращение критерия качества системы. Получим соотношение для вычисления такой оценки [50]. Матрицу коэффициентов передачи обратной связи для реальной системы можно записать в виде

Dp(0=D(0+AD(0. (5.19)

В этом случае уравнение (5.5) примет вид

x(O = [A(0-B(0Dp(0]x(0=Ap(0x(0. (5.20)

где Ap(0=A(0-B(ODp(0.

Начало

A,B,B,N,R,

А„=А-ВГ

Вычисление матрицы А, RE(K), 1М(К). SP EVCPB 31

1 = 7

AyA-BJij

Вычисление si, матрицы Ay: REO(K), ТМО(К)- SP EVCPD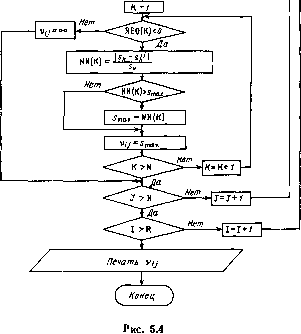

Критерий качества (5.2) для системы (5.20) с реализованными обратными связями и при Фк = 0 имеет вид

фр(0 = Ф+ор(0ЧОр(0-

(5.21)

Представим критерий качества (5.21) в виде квадратичной формы

x(ON(Ox(0= /"х-(т)ФрХ(т)т, (5.22)

где H{t)-положительно определенная симметричная матрица, пока неизвестная. Продифференцировав выражение (5.22), с учетом (5.20) получим:

хУ{1) А-р (О N (Ох(0 +х(О N (Ох (О +

+х- (О N (О Ар (О X (О =-х (О Фрх (О (5.23)

Равенство (5.23) должно выполняться при любых значениях вектора фазовых координат. Поэтому, заменив Ар (О ее выражением из (5.20), находим;

-N(0=A-(ON(0 + N(t)A(0-D-p(OBMON(0-

-N(0B(0Dp(0+Op(0, N(4)=Фк, (5.24)

где Фк - граничное значение.

Для системы с оптимальным регулятором имеем [6]

/(Uo) = l/2x-(0K(0x(0, (5.25)

где К (О -решение матричного уравнения Риккати:

K(0=A-(OK(0 + K(OA(0-D(OBMOK(0-

-К(0В(0О(:0+Фо(0. К(М=Фк. (5.26)

в котором Фо{t) =Ф -Ь {t){t).

Обозначим AK(0 = N(0-К(0- Вычитая почленно (5.26) из (5.24), получим дифференциальное уравнение для вычисления матрицы ДК(0"-

-АК(0 = [АЧОВМО-AD40 В(0 ] АК(0+ -ЬАК(0[А(0-В(0О(0-B(OAD(0] +

+AD(0FAD(0, АК(/к)=0. (5.27)

Если в квадратичном функционале (5.2) о=0, 4 = оо, а в уравнении i(5.1) tMaTpHHbi А (О и B{t) постоянны, то ДК=const, и дифференциальное уравнение (5.27) преобразуется в алгебраическое

(А-DpB) AK-fAK(A-BDp)=-АОЧДО. (5.28)

Это уравнение для устойчивой системы при любой матрице в правой части имеет единственное решение [11]. Тогда приращение критерия качества вычисляется по формуле

A/ = /(Up)-/(Uo)=V2X(0)AKx(0). (5.29)

Подпрограмма DOMIN

Назначение: вычисление коэффициентов чувствительности. Обращение: CALL DOMIN (А, В, D, N, R, MU).