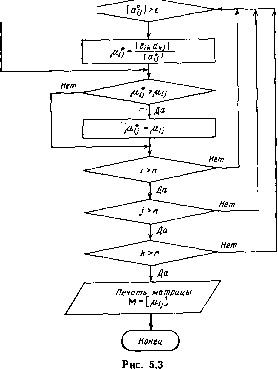
DIMENSIOM МН,Н) ,0«Ш) Л1С6) ,FIMIH(6) ,FIHAXC6) ,FIHSC6)

LOGICAL*! CTPOKA( 1в1),SI, SF, ST,SB,SSC6)

DATA CTFOKA/ieiKlH /,SI,3P,ST,SB/1HIДН+,1Н-ДК /

DATA SS/lH»,lH*,lH&,lHtMH>:,lHZ/,11/1,2,3,4,5,6/

IF .tt.GT.6.0F;.tt.LE.e.0R.N.LE.e) RETURN

DO 1 L=l,«

FIMINCL) = A(1,L) FIMAX(L) = Aa,L) DO 1 1=2, N

IF ( A(I,L) .GT. FIMAX(L) ) FIMAX(L) = A(I,L) IF i A(1,L) .LT. FlMIHiU ) FIMINCL) = A(I,U iCOHTlNUE 33 FORriATUH ,Т1в,11/-Й ГРАФИК (СИМВОЛ - ,A1,)/)

DQ 66 KK=1,M 66 FIMSCKK) = <Е1МАХ(КЮ-Е1МШКК))/1вв.

PRINT le,(IKKIC),FI«IN(KK),Ii(KK;,FIMAX(KK),КК=1,И> PRINT 33,(II(I),S3CI),I=1,M) DQ 2 1=1,N

HO 3 j=i,iei,ie

CTP0KA(J)=3I 3 CONTINUE

IF ( 1-1/1вк1в .NE. 1 ) GO TO 5 DO 4 J=l,91,ie

СТРОКА (J) = SP DO 4 K=l,9 L = JK CTPOKA(L) = ST

4 CONTINUE

5 DO 55 KK=1,«

К = INT( ( A(I,KK)-FININCKK) ) / FIi13(KK)+i.5 55 CTPOKA(K) = .SS(KK)

IF ( I-I/ie»ie .NE. 1 ) GO TQ 6 PRINT 28, OIK I), (CTFOKA( K), K=l, 1в1) 00 ТО 7

6 FTINT Зв,(СТР0КА(К),К=1,1в1)

7 DO 2 K=l,iei

CTFOt(K) = SB 2 CONTINUE

le FQRMATdH ,/T15,MIN , II,-,Gie.4,54X,MAX Ml,-,01в.4) 2в F0RMAT(lX,G12.6,ieiAl) ов F0RMAT(13X,ielAl)

FiETURN

5.4. ВЫДЕЛЕНИЕ ДОМИНИРУЮЩИХ ОБРАТНЫХ СВЯЗЕЙ В ОПТИМАЛЬНОЙ СИСТЕМЕ

Реализация оптимального управления для систем высокой размерности вызывает определенные трудности. Они связаны с необходимостью введения большого количества обратных связей, которые для нестационарных систем переменны во времени. Поэтому представляет интерес задача упрощения структуры оптимального регулятора. Эта задача особенно актуальна для непрерывных систем управления, так как практическая реализация каждой связи с переменным коэффициентом усиления является довольно трудоемким процессом. Для ее решения необходимо выявить те связи, которые несущественно влияют на качество регулирования и которые можно отбросить, практически не изменив динамических свойств системы. Рассмотрим два возможных способа выделения таких связей [66].

Способ 1. Основан на исследовании влияния каждой обратной связи на элементы матрицы динамических параметров оптимальной замкнутой системы Ао= [a°ij(0] в уравнении (5.5).

Связь между элементами матриц динамических параметров исходной и оптимальной систем в скалярной форме имеет вид

all it) = atj {t)-i 6,., (О d„ (t). (5.14)

При обрыве обратной связи с /-й фазовой координаты на 1-е управление элемент dij{t) становится равным нулю. Поэтому элемент a*ij{.t) матрицы, полученной из Ао(0, будет равен

4(0 = «гИ0- i biAt)duM (5.15)

Определим относительное изменение элементов матрицы Ао(0 при отбрасывании обратной связи dij{t):

\a1j(t)-a]{t)\ \bii(t)di}{t)\

a?/(Oi la?/(01

(5.16)

Из выражения (5.16) видно, что обратная связь с коэффициентом dij влияет только на элементы /-го столбца матрицы Ао(0-Для оценки влияния обратных связей на значения элементов матрицы Ао(0 введем коэффициент чувствительности системы к параметру dif

\Ьц {t)du{t)\

Li;; = max max -----. (5.17)

Если некоторые элементы матрицы Ао(0 принимают нулевые значения, их необходимо приравнять малому числу е, абсолютная величина которого зависит от точности задания элементов исходных матриц A{t) и B{t).

Следует заметить, что в силу теоремы о непрерывной зависимости решения системы дифференциальных уравнений от параметров, достаточно малое изменение начальных условий и правых частей уравнений приводит соответственно к малым изменениям решения на всем исследуемом отрезке. Однако не всегда решения, близкие по начальным условиям, остаются близкими при сколь угодно больших значениях аргумента, т. е. с возрастанием аргумента, вообще говоря, различие между двумя интегральными кривыми может увеличиваться. Поэтому при отбрасывации обратных связей, изменяющих матрицу динамических параметров системы, необходимо выполнить проверку полученного решения, например путем моделирования на ЭВМ.

Таким образом, получаем следующий алгоритм исследования влияния обратных связей на свойства оптимальной системы:

1. Вычислить матрицу коэффициентов передачи обратных связей D{t) по формуле (5.3).

2. Вычислить коэффициенты чувствительности системы [iij по формуле (5.17) для всех обратных связей и составить из них матрицу коэффициентов чувствительности fA=[\iij].

3. Задавшись некоторым положительным числом б, выбрать все коэффициенты для которых }a;j<;6; значение 6 целесообразно выбирать в пределах 0,05... 0,1. Будем предполагать, что такие связи слабо влияют на динамические свойства оптимальной системы (назовем их несущественными).

4. Отбросив несущественные связи, необходимо проверить, насколько измененная система отличается от оптимальной.

Для вычисления матрицы коэффициентов чувствительности М составлена подпрограмма DOMIN, реализующая алгоритм, схема которого приведена на рис. 5.3.

Г Начало \