С Начало \

Исходные данные

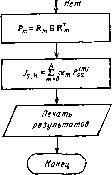Рис. 3.3

ки для многомерной системы (3.41). При этом алгоритм будет следующим:

1. Интегрирование дифференциального уравнения исследуемой системы (3.41).

2. Вычисление матриц Ri, R2,... , по формулам (3.44).

3. Вычисление матриц Ро, Pi,..., Р путем интегрирования матричных выражений (3.49).

4. Вычисление искомых оценок /i,*, h,h,... , Jr.h ПО формулам (3.51).

Для системы, имеющей г выходных переменных, вычисляется г матричных интегралов (3.49). Поскольку для стационарной системы Rm = const, то вычисления можно упростить. Действительно, при оговоренных условиях равенства (3.49) принимают вид

Pm = jRm x it) х- it) R; dt = R,„ GR;,

m = 0, 1,..., где (лХл)-матрица

(3.52)

(3.53)

G= Jx(0 x(0 dt.

Следовательно, в алгоритме достаточно предусмотреть вычисление интеграла (3.53), тогда матрицы Pm определяются по (3.52) умножением G слева на Rm, а справа

на Ят.

Схема алгоритма представлена на рис. 3.3. Входными данными алгоритма являются матрицы А, С уравнения модели, параметры От интегральных оценок (ао=1), Т - правая граница интервала интегрирования и другие величины, необходимые для организации вычислительного процесса.

ГЛАВА 4

СЛУЧАЙНЫЕ ПРОЦЕССЫ В УПРАВЛЯЕМЫХ СИСТЕМАХ

При проектировании систем автоматического управления различного назначения обязательным является исследование точности работы систем при наличии случайных воздействий - статистический анализ. Статистический анализ сводится, как правило, к вычислению средиеквадратических ошибок, корреляционных функций и спектральных плотностей для управляемых координат. Ука-

занные характеристики вычисляются .для линейных систем на основе корреля-щионной теории случайных процессов. Причем оценки точности получают как по спектральным и частотным характеристикам, так и по специальному алгоритму, позволяющему найти требуемые показатели в результате интегрирования дифференциальных уравнений, записанных для вторых моментов координат управляемой системы.

Рассматриваются также вопросы моделирования случайных процессов. Представлен алгоритм формирования стационарных случайных последовательностей, имеющих экспоненциальную корреляционную фун!4цию. Изложена методика построения алгоритма, с помощью которого может быть получен процесс с произвольным дробно-рациональным спектром.

4.1. ОПРЕДЕЛЕНИЕ ДИСПЕРСИИ ВЫХОДНОЙ ПЕРЕМЕННОЙ СТАЦИОНАРНОЙ ЛИНЕЙНОЙ СИСТЕМЫ ПО СПЕКТРАЛЬНОЙ ПЛОТНОСТИ

Будем рассматривать стационарную линейную систему с передаточной функцией

W{p)Bip)/A(p). (4.1)

Пусть на вход системы поступает стационарный центрированный случайный процесс x{t), имеющий спектральную плотность Sx(cu). Выходную переменную системы обозначим через y{t). Требуется определить установившееся значение дисперсии Оу выходной переменной у исследуемой системы.

Спектральная плотность реакции системы (4.1) 8у(и)) на x{t) в установившемся режиме определяется по формуле

Syia) = \Wii(D)\S4<D), (4.2)

где квадрат модуля частотной характеристики

r(jco)P=U7(jco)r(-j«). (4.3)

При этом дисперсия y{t)

" 2я

II(J«)i5,(«)dco. (4.4)

Рассмотрим алгоритм вычисления дисперсии Оу для случая, когда спектральная плотность Sx(a) аппроксимируется дробно-рациональной функцией 5х((о) =ФОсй)Ф(-jffl). При этом функция 0{p)=G{p)\/R{p) имеет нули и полюсы, расположенные в левой полуплоскости.

С учетом (4.1) - (4.4) выражение для дисперсии выходной переменной примет вид

" 1-2я Д А(р)А(-р)

где многочлены

A{p)=A{p)R{p); B{p)=B{p)G{p). (4.6)

3* 67

Для вычисления интеграла (4.5) воспользуемся эффективным алгоритмом, обоснование которого приведено в [61]. Примем

Ап(р) =А(р) =ao"p" + aiP"-4-... +а%; 5„(р)=Л(р)=6»,р»-1+ ... +6%.

Введем в рассмотрение полиномы Ah(p) =ahp+a\pf-+ ... +ah;

Bk(p)=bhp-+ ...+bh, (4.7)

коэффициенты которых определяются из рекуррентных уравнений Ak-i (р) = (р) -OftAft (р); fift-i (p)=Sft(p)-.pftI,(p),

где aft=cVai; Pft = &Vai; Мр) = [МР)~{-)Ли{-р)]/2. Введем в рассмотрение также интегралы

i 2я Д (;>) Лй ( - р)

где полиномы Ak(p), Bh{p) определяются формулами (4.7). Тогда при условии, что все корни полинома А{р) лежат в левой полуплоскости, справедливы рекуррентные соотношения

4=/ft-i + PV(2aft), =1, .... п; /о = 0.

Чтобы найти значение интеграла 1п = иу, необходимо вычислить коэффициенты полиномов Аи, для k = n-1, 1. Это можно сделать с помощью следующей таблицы:

al a\

ai 0

b\ a\

Каждая четная строка в таблице коэффициентов а получается сдвигом элементов предшествующей строки влево и соответствующей подстановкой нулей. Четные строки правой части таблицы идентичны строкам ее левой части. Элементы нечетных строк по-