Из (2-5) имеем:

l+-r/2. .ll(i -№)

(2-36)

(2-37)

Выражение (2-27) можно проверить другим способом, определяя коэффициент мощности основной составляющей схемы следующим образом. Из (2-27) имеем:

10 =

(2-40)

1 + е"!

Коэффициент мощности основной составляющей определяется следующим образом:

«в(1) (О = 1 sin со/ 4- Вг cos со = Y а\ -\- sin (<t - 9),

(2-41)

где tg.=-

Считая волны симметричными для каждого полупериода, получаем:

Л» = j EaiKr,-2Кг,е-")sin<.tdt =

= \ (Кг, sin с4 - 2/С„е~" sin «/) dt =

о 4Ed

/Сю COS cof

-2/С„е

-t/iRC

2 25„.- (со)

(- со)

(4Дс)

г -1-со

(2-42)

4£d

-Щ- cos ci>< -b CO sin coi

co-b

4£d

со-Ь

4RCr[,o--()

(g-r/8KC l). (2-43)

Из (2-42) и (2-43) имеем:

-Time

+ 1)

2/CnCO

<o= +

,-TISHC

4-1)

/С„со

Из (2-40) имеем

Таким образом, tg9 =

Это совпадает с выражением (2-48) этой главы.

(2-44)

ГЛАВА ТРЕТЬЯ

ПОСЛЕДОВАТЕЛЬНЫЕ ИНВЕРТОРЫ

Инвертор с последовательным подключением коммутирующего конденсатора имеет последовательную резонансную цепочку L, С, обеспечивающую коммутацию. У большинства основных схем инверторов в момент запирания тиристора возникает пульсирующий ток колебательного характера. Резонансная частота схемы определяет продолжительность прохождения затухающего синусоидального импульса тока через тиристор, резонансную цепочку и нагрузку.

В данной главе излагается работа основной схемы инвертора с последовательным подключением коммутирующего конденсатора, включая расчет с определением кривых напряжений и токов в установившемся режиме. Далее рассматриваются некоторые модифицированные однофазные схемы. Эти схемы расширяют рабочий диапазон основной схемы последовательного инвертора.

Некоторые однофазные и многофазные схемы показаны дополнительно для иллюстрации разновидностей инверторов с последовательным подключением коммутирующего конденсатора.

Простой последовательный инвертор, работающий на сравнительно стабильную нагрузку, может создавать на ней напряжение с формой кривой, очень близкой к синусоиде. Когда ток нагрузки увеличивается, амплитудное значение напряжения на конденсаторе возрастает. К схеме простого последовательного инвертора могут быть добавлены цепи обратной связи, облегчающие решение этой задачи и увеличивающие практический диапазон рабочих нагрузок.

Вообще говоря, последовательный инвертор может отключаться более легко, чем параллельный, так как

в этом случае нет необходимости включать тиристор. Чтобы запереть другой тиристор, находившийся ранее в проводящем состоянии. Можно разорвать цепь управляющего электрода тиристора и тем самым прекратить работу инвертора. Благодаря этому исключается необходимость в ряде случаев иметь выключатели в силовой цепи, так как инвертор может быть включен и отключен соответствующими переключениями в цепи управляюпде-го электрода, хотя следует предпринять некоторые меры, исключающие нежелательные переходные процессы при пуске.

3-1. ОСНОВНАЯ СХЕМА ПОСЛЕДОВАТЕЛЬНОГО ИНВЕРТОРА

Основная схема инвертора с последовательным подключением коммутируюидего конденсатора показана на рис. 3-1.

Термин «последовательный инвертор» используется для обозначения инвертора, который коммутируется конденсатором, включенным последовательно с нагрузкой.

Когда в схеме рис. 3-1 тиристор Tt открыт, а тирнстор Т2 закрыт, последовательная резонансная цепочка подсоединена по существу к источнику питания постоянного тока. Еслн в схеме нет потерь, т. е. соблюдается условие /?н = 0, то напряжение на конденсаторе за время первого полупериода колебания возрастает по синусоиде до величины, равной 2Еа. Затем прохождение тока прекращается, так как ток падает ниже величины то-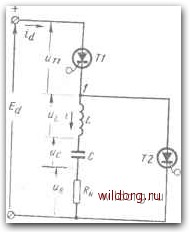

Рпо. 3-1. Основная схема инвертора с последовательным подключением ко.м.мутирующего конденсатора.

дает ниже величины тока удержания тиристора. Синусоидальная полуволна тока достигает максимума в тот момент, когда конденсатор заряжается до напряжения, равного Еа, и 58

спадает к нулю, когда напряжение на конденсаторе становится равным 2Ed. В течение второго полупериода работы инвертора, когда тиристор Т2 открыт, эквивалентная схема опять имеет вид той же последовательной резонансной цепи, но уже без источника питания постоянного тока, и с начальным напряжением на конденсаторе, равным 2Еа. По цепи вновь протекает ток в виде синусоидальной полуволны противоположного направления, а конденсатор заряжается с отрицательным напряжением до величины 2Еа, если предположить, что R=0. Когда тиристор Т1 включается вновь, то условия становятся такими же, как и во время первого полупериода, за исключением того, что начальное напряжение на конденсаторе равно отрицательной величине 2Еа, а не нулю. Если пренебречь потерями, то можно считать, что к концу третьего полупериода напряжение на конденсаторе становится положительным и равным 4£d. Такая работа продолжается последовательными полупериодами, и при условии, что i?h=0, напряжение на конденсаторе будет все время возрастать от периода к периоду. Практически в цепи имеются сопротивления нагрузки и потерь, что предотвращает последовательное удваивание напряжения на конденсаторе. Отношение индуктивного сопротивления или емкостного сопротивления Хс К активному сопротивлению R есть добротность Q цепи. Основная гармоника напряжения на конденсаторе возрастает по экспоненте до установившегося значения с постоянной времени, равной Q/л периодов, если схема работает с ее .резонансной частотой.

Важным свойством схемы рис. 3-1 является то, что она, строго говоря, будет работать только в том случае, если ток равен нулю в течение интервала времени, требуемого для восстановлення управляющих свойств тиристоров в конце каждого полупериода работы. Соблюдение этого условия необходимо, чтобы тиристоры были в состоянии восстановить свою способность запираться в прямом направлении в конце каждого полупериода проводимости.

3-2. РАСЧЕТ СХЕМЫ

Расчет схемы рис. 3-1 можно выполнить, решая дифференциальные уравнения, описывающие процессы, протекающие в схеме. Этот расчет приведен в § 3-5. Если