рис. 1-3 (см. гл. 1). Угол опережения схемы, т. е. промежуток времени, следующий сразу после интервала проводимости, в течение которого к вентилю прикладывается отрицательное напряжение, равен фазовому углу, соответствующему коэффициенту мощности. В действительности эта аппроксимация вполне удовлетворительна

Рис. 2-4. Эквивалентная схема инвертора по рис. 2-2 для каждого по-лупериода.

И ДЛЯ формы кривой выходного напряжения, значительно отклоняющейся от синусоиды, что будет показано в соответствующем параграфе.

Расчет схемы [Л. 2-3 и 2-4]

Подробный расчет схемы рис. 2-2 может быть выполнен путем решения дифференциальных уравнений, описывающих ее работу. Однако, как показано в § 2-3, такой расчет очень сложен, даже если не учитывать колебания питающего тока и индуктивность в цепи нагрузки.

Окончательные соотношения для схемы с большим дросселем в цепи постоянного тока и незначительной индуктивностью нагрузки имеют следующий вид:

£,(l+e-r/2T 2e-b)

.-ЦТ

(1-.-/)

(2-27)*

(2-35)

* Номера формул, не встречавшихся ранее в этой главе, соответствуют номерам выражений, выведенных в § 2-3, где приведен подробный расчет схемы рис. 2-2. (Прим. автора.)

1 + ,-да (1 ,-т/2.)

(2-36) (2-37)

где x=4RC.

Влияние на напряжение на нагрузке изменений активного сопротивления нагрузки и емкости коммутирующего конденсатора можно определить, подставляя различные численные значения т в равенство (2-27). На-

пример, при x = 4RC=-.

Еа(1--е--2е-*<) £rf(l +0,05 - 26-)

i+e--~(\-e-)

=. 3£Л1.05-2./°) f,(2,52-4,80«); 1,25

"нМ = -2,28£-d; и„ \t=Ti2 = Еа (2,52 - 4,80-= 2,28£-<г.

При xarc =

-- 1 ~ 2 4 -

1-1----(1 --) T""T~

= 3£Л1.СЮ25-2.-Я/)) 5 2,99e-/(/2));

u„ l;=o = - l,49£<j. Ha рис. 2-5 показаны формы кривых напряжений на нагрузке и на тиристоре для

т<7-/2, т=7/12 и т=Г/6.

Как показано на этом рисунке, увеличение активного сопротивления нагрузки или емкости коммутирующего конденсатора существенно изменяет форму кривой и величину максимального значения напряжения на нагрузке. Максимальное напряжение на нагрузке должно увеличиваться, когда увеличивается ARC, так как площади, показаные на рис. 2-5, должны оставаться равными.

Если эти площади равны, то Un - среднее значение напряжения на нагрузке за время интервала проводимости каждого тиристора - равно Ed, так что на Ld нет постоянного напряжения.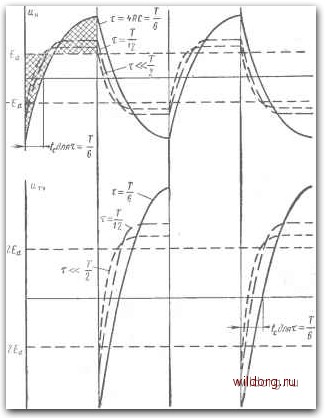

Рис. 2-5. Формы кривых в схеме рис. 2-2 без учета индуктивности цепи нагрузки при большом дросселе в цепи постоянного тока.

Наиболее важной частью периода является время опережения, т. е. время, в течение которого напряжение на тиристоре бывает отрицательным после интервала проводимости. В параллельном инверторе, у которого можно пренебречь реактивным сопротивлением в коммутирующей цепи, интервал времени, когда действует отрицательное анодное напряжение, является по существу 32

полным временем опережения. Этот интервал времени должен быть достаточным, чтобы тиристор смог восстановить свою способность запираться в прямом направлении. Как видно из рис. 2-5, этот промежуток времени увеличивается с ростом активного сопротивления нагрузки или коммутирующей емкости. Это означает, что для данной нагрузки коммутирующая емкость должна быть тлкой, которая требуется для обеспечения необходимого времени опережения.

Время опережения 4 можно рассчитать для случая неизменной величины тока питания при чисто активной нагрузке, приравнивая выражение (2-27) нулю. А именно:

,-Г/2т

(2-38)

с

-f 1

Время опережения, выражешюе в радианах, т. е. угол опережения, будет:

Как уже указывалось ранее, угол опережения может быть очень близко аппроксимирован фазовым углом коэффициента мощности схемы для основной гармоники, если даже напряжение на нагрузке существенно отличается от синусоидального. Это можно проиллюстрировать следующим образом:

Реактивный ток основной гармоники =

Активный ток основной гармоники =

и

tg9i=-77-

3-1503

(2-45) (2-46)

(2-47)

Пренебрегая индуктивностью нагрузки, получаем:

tg4)i=4coi?C. (2-48)

В табл. 2-1 приведены величины р и фь найденные из равенств (2-39) и (2-48).

Таблица 2-1

Сравнение точного и унрощениого способов расчета угла коммутации

Как показано в § 2-3, выражение для напряжения на нагрузке в самой общей форме, т. е. для случая малых значений La и при включении индуктивности в нагрузке, получается очень сложным. При этих условиях одно из решений может быть получено обратным преобразованием равенств (2-17) и (2-18), данных в § 2-3. Для случая, когда сопротивление нагрузки чисто активное и La ограниченно, из равенства (2-18) имеем:

"н = /Сл + /Све-"" sin {t -f ФО-

(2-49)

Если в нагрузку включена индуктивность, то из выражения (2-17) следует:

«н = /(с + Ко е-ъ* + Ке e-Tf» sin (a,,f -f ф,). (2-50

Полный анализ этих равенств очень сложен.

Для большинства практических случаев задача сильно упрощается с помощью приближенного анализа с использованием тех основных принципов, которые рассмотрены выше. Если нагрузка имеет сравнительно большую индуктивность, то в большинстве практических случаев имеем форму кривой напряжения на нагрузке, 34

близкую к синусоидальной. Для этого случая приближенный анализ дает следующее:

/d.iHeSinf = d.rlfHfCOS?:

1 1

(2-3) (2-51)

R и Xl -эквивалентные параллельные активное и индуктивное сопротивления в схеме рис. 2-3.

(2-1)

Для тока с прямоугольной формой кривой

V2T .}

COS (at

со Jo

r/2 212 г - -Jd-

(2-52)

Объединяя выражения (2-3) и (2-51), получаем:

/ /d..i J I

if del

(2-53)

R + Xc

Объединяя выражения (2-1) с (2-52) и (2-53), получаем:

,2 8 ,2 R"C

а также:

8 R Хс

Vr- + x

U,,,. = VH,.IaR-- = Ea

(2-54)

(2-55) 35