ческий эффект. Соображения по габаритам и стоимости являются также важными факторами, когда выбираются величины Li и Ci для конкретного случая. Во многих схемах инвертор содержит изолировочный трансформатор, реактивное сопротивление рассеяния которого может оказаться удобным добавком к реактивному сопротивлению фильтра. В низковольтных применениях установленная мощность конденсаторов может определиться экономически обосно-ванны.\1 минимальным номинальным напряжением изготовляемых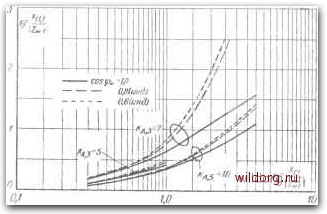

Рис. 7-16. Кривые зависимости индуктивности реактора фильтра от величины емкости фильтра для различных ослаблений и гармоник, построенные по уравнению (7-54).

конденсаторов. (Конденсаторы спроектированные для низких напряжений, требуют, чтобы снизить их размеры, ультратонкой бумаги.) Эти н другие соображения не могут быть оставлены без вяи.мания при проведении технико-экономической оценки, необходимой при проектировании конкретного фильтра.

Многозвенный фильтр LC

Когда требуется более высокая степень ослабления гармоники, становится желательным применение многозвенных фильтров LC-типа, рассмотренных в предыдущем разделе. Двухзвениый фильтр LC с той же самой установленной мощностью емкости и индуктивности, как и в однозвенном фильтре, имеет гораздо более значительные возможности ослабления. Это основное свойство выражено тем сильнее, чем больше звеньев в фильтре. В подавляющем большинстве фильтров, однако, потребность в ослаблении гармоник удовлетворяется не более чем двумя звеньями. Приблизительная величина ослабления, при которой двухзвенный фильтр предпочтительнее однозвенного, устанавливается в данном подразделе.

Прежде чем входить в детальный анализ двухзненного фильтра, интересно рассмотреть некоторые факторы, которые могут оказать влияние па решение о применении многозвенного фильтра. Прежде

„ пппбпяженпя но устойчивости системы. Когда приме-всего °"Р„Лет систему автоматического регулирова-

ненньш фильтр в"™"" "l.-na наличие двух четырехполюсников ния «спряжения замкнутого тип Д У Эту

cбTe:>"rн"нe-™с°.яГи?ь повышением резонансной че-

i „о D д пячя или

; иг I

npco.ic-u -------

стоты фильтра в 4 раза или более.

Другим соображением являются габариты и стоимость фильтра. Хотя каскадный фильтр может теоретически показаться желательным при некоторой величине ослабления с точки зрения сведения к минимуму общей установленной мощности, однако габариты н стои.мость добавочных элементов могут повысить ве-

лич1шу ослабления, при которой каскад фильтров становится выгодны.м.

Передаточная функция для двухзвенного фильтра, показанного на рис. 7-17, определяется следующим путем;

/н(Р)-/н(Р)/?н=/4(Р)

Рис. 7-17. Двухзвенный фильтр.

(7-55) (7-56)

/з(р)-=

pCi иЛр)

--йГ" •

Подставляя (7-56) в (7-57). получаем:

t/г (Р) = -~--Rn

(7-57)

(7-58)

(Р) =

(7-59)

Это конечно, та же передаточная функция однозвенного фильтра LC, которую мы получили выше. Ток h определяется из

Подставляя (7-58) в (7-60). получаем:

h (Р) = /Cit/h (р) (PUC, ++)-

(7-60)

(7-61) 229

Ток Ii определяется выражениями

U{p)=h(p)+/3ip). (7-62)

U,,(p)pLJi{p)+U,ip). (7-63)

Тогда из уравнения (7-58) при использовании (7-63) получаем:

Uu (р) и„ (р) [pCL, (pL,C, ++ l) + + PiC, +

(7-64)

Несколько примеров расчетов ослабления для одно- п многозвенных фильтров приводят к интересным соображениям. Ослабление однозвенного фильтра LC, показанного на рис. 7-6, может быть определено следующим образом. Принимая полное сопротивление цепи для пятой гармоники Xi,i=/1 000 и Xci=-/50, получаем ослабление:

Un . -/50 -/50 1

t7„ /1 000-/50

/950

Ослабление многозвенного фильтра, показанного на рис. 7-17, и,меющего ту же самую установленную мощность элементов фи.тьт-ра, но разделенную на две части между включенными каскадом двумя звеньями LC, может быть подсчитано следующим образом. В этом случае сопротивления для пятой гар.чоники равны:

Х1,1=Л:ь2=/500; Kci=Xci=r-im

и ослабление будет равно:

/ 400 (-/ 100) -/100 /400-/ 100

(,ш) =

/500-/100 .

/ 500 +

] 400 (-/ 100)

/ 400 -/ 100 1 1 1

-/ 133

500-/ 1.33 Г "2775 ГГ

Таким образом, многозвенный фильтр обеспечивает меньшее чем одноступенчатый фильтр ослабление при той ке самой суммарной мощности элементов.

Если параметры элементов выбираются такими, чтобы получить сопротивления следующего порядка: Ai,i=/2 000 и Xci = -/25 то ослаоление для однозвенного фильтра составит-

-/25

/ 2 ООО - / 25 79

Соответствующ.че параметры элементов для многозвенного фильтра составят:

Xi,i-A-i,2=/l ООО; Хс1 = Хс2 = -/50, и ослабление будет равно

/ 950 (-/ 50)

On .. . -/50 /950-/50

(/ш):

" / 1 ООО - / 50 .

/950 (-/50)"

-/53

;1000-f у у 50 19 \ 17,еу 34

19/1 ООО -/53"

демонстрируя, что многозвенный фильтр при этих уровнях ослаблений значительно превосходит аднозвенный фильтр.

Очевидно где-то между этими крайними случаями однозвенный и Многозвенные фильтры эквивалентны. Знание уровня ослабления, при KOTopOiM оба фильтра эквивалентны, по.могаег при решении вопроса, когда оправдано использование многозвенного фильтра для данного при.менения.

В качестве примера типичного расчета, требующегося для определения ослабления, при котором двухзве.чный и однозвенный фильтры эквивалентны, предполагаем, что фильтр, показанный на рнс. 7-17, имеет равные величины индуктивностей и емкостей, каждая из которых равна по.товине соответствующей величины в одно-звенном фильтре:

Li - индуктивность однозвенного фильтра; Cl - емкость однозвенного фильгра; Ln=L22 - индуктивность двухзвенного фильгра; Cii = C22 - емкость двухзвенного фильтра;

Z.,, = Z.22 = 2

Сц = Саг - 2

(7-65)

(7-66)

Передаточная функция однозвенного фильтра LC в режиме .холостого хода равна:

иР- pL.c.-f 1

Передаточная функция многозвенного фильтра LC в режиме холостого хода с учетом соотношений (7-65) и (7-66) равна:

(7-67)

(7-68)

Переходя от передаточных функций по уравнениям (7-67) и (7-68) к функции /со и применяя соотношения между величина-мя 16» 231

Ll, С, II резонансной частотой £.)с, получаеч-

0. . 1

(для однозвенного фильтра);

а>2

(7-60)

On 1

16<0„

(для двухзвенного фильтра). (7-70)

лентнк,*" ""•«"«я ослабления, при котором оба фильтра эквивалентны, левые части выражений (7-69) и (7-70) приравниваются:

3 052 ---2+1]

(7-71)

Когда W больше, чем шс, выражение в левой части равенства

может быть записано в виде будут положительными:

-- 1

, так что обе части уравнения

3 со2

16соо

м* 7 в)2

-4-х-2+2=0.

16(0;

(7-72) (7-73)

Решая это уравнение относительно о)/шо и подставляя получен-ление ГЛ уравнение (7-69) или (7-70), можно найти ослабление, при котором оба фильтра эквивалентны:

14+ 12,8 .

(7-74)

Полученное соотношение показывает, что два фильтра эквивалентны в двух случаях. На самом деле меньшая величина ю/соо исключается, поскольку эквивалентность в Э10м случае лежит в об-

/ со \г

ласти резонансного пика. Величина ( =26,8 представляет нужный результат. Подставляя эту величину в (7-69), получаем:

О") = -26,8+1 ~~25 25,8 £ 180° (")

Уравнение (7-75) показывает, чго при применении фильтров, где требуется ослабление до величины 26:1, самым желачельным является применение однозвенного фильтра. В случаях, когда требуются ослабления больше, чем 26:1, следует рассмотреть многозвенный фильтр. Важно 01метить, что эти зак.чючения проистекают из специфичности случая, когда нагру.кой иа выходе фильтра можио пренебречь и когда части каскада фильтра принимаются иден-232

тнчнычн друг другу. Кроме того, следовало бы подчеркнуть, что многие практические соображения будут влиять на решение, применять ли в данном случае однозвенный нли двухзвенный фильтр.

Резонансные фильтры

Главные недостатки простых фильтров LC заключаются в дополнительном паде:-1Ии напряжения в последовательном элелгенте и в повышенной нагрузке инвертора за счет параллельного элемента. Резонансные четырехполюсники в последовательном и параллельном элементах могу г частично компенсировать эти недостатки. Например, последовательная резонансная цепь, как показано на рис. 7-18,а, настроенная в резонанс с основной частотой, сводит к минимуму падение напряжения от тока основной частоты.

На рис. 7-18,6 показана параллельная резонансная цепь, использованная в качестве параллельного элемента для понижения дополнительной нагрузки на основной частоте. Параллельная резонансная цепь представляет собой большое полное сопротивление для основной частоты и имеет в то же время малое емкостное сопротивление для более высоких гармоник. Комбинация обеих резонансных цепей (рис. 7-18.е) объединяет преимущества их обеих.

Применение резонансных фильтровых цепей ограничивается теми случаями при.менения, когда имеется возможность работать с фиксированной или почти фиксированной частотой.

Рис. 7-18. Резонансные фильтры.

а - последовательный резонансный контур в последовательном элементе фильтра; б - параллельный резонансный контур в параллельном элементе фильтра; в - сочетание последовательного н параллельного резонансных контуров в последова-1ельном и параллельном элементах фильтра.

7-4. МНОГОФАЗНЫЕ ИНВЕРТОРЫ

Многофазные схемы обеспечивают возможность сведения к минимуму гармоник в выходном напряжении инвертора. Прямоугольная крнвая выходного напряжения простого и.мпульсно-коммутируе-мого инвертора преобразуется в многофазной схеме так, что требования к внешним фильтрам снижаются. Многофазная схема либо обеспечивает гашение определенных гармоник, либо приводит к по-вьпнению основной гармонической составляющей относительно определенных гармоник. Так как в большинстве случаев применения мощных инверторов требуется трехфазная система напряжений, то в кривой напряжения отсутствуют третья гармоника и кратные ей. Когда применяются схемы с большим числом фаз, исключаются и другие rapMOHjJKH.