практнчеоких фильтров при использовании полных сопротивлений каждого элемента фильтра, а затем подсчетом отношения полных сопротивлений цепи согласно (7-15).

Влияние величин L и С на работу фильтра

Общим является то, что когда фильтр LC достаточно ослабляет низшие гармоники, имеющиеся в напряжении инвертора, более высокие гармоники одновременно понижаются до допустимого уровня. Это получается потому, что практически фильтры обычно выполняются так, чтобы их резонансные частоты «с были ниже самой низкой гармоники, которая должна быть ослаблена. Таким образом, данные гармоники возникают в диапазоне частот, когда характеристика ослабления фильтра имеет спад 40 дб1дек, как показано на рис. 7-7. Форма частотной характеристики показывает, что ослабление при данной частоте определяется ее отношением к резонансной частоте фильтра.

Отаосительно просто определить произведение LiC\, требуемое для данного ослабления гармоники до определенной величины. Однако величины Li и Ci остаются все еще не определенными. Два важных параметра фильтра, которые зависят от фактических значений Li и Ci, даются ниже.

1) снижение напряжения основной гармоники UiJUui;

2) относительная величина тока инвертора /hi hi.

Большая величина Li и малая величина Ci дадут большое снижение напряжения основной гармоникп напряжения, а величину тока инвертора - лишь слегка большую величины тока нагрузки.

С другой стороны, малая вели-/ чина Li и большая величина

Cl будут сказываться в малом снижении напряжения основной гармоники напряжения, а также в значительном возрастании тока инвертора по сравнению с током нагрузки. В любом случае это неблагоприятно оказывается на номинальных данных инвертора. Таким образом, требуется технико-экономическая оценка. Важное значение в этой технико-экономической сценке нмеег коэффициент мощности нагрузки.

При проведении требуемой технико-экономической оценки следует Б первую очередь изучить взаимоотношение T-i и Ci и их воздействие яа инвертор. Хотя результаты этой оценки не могут обеспечить способа нахождения опти.муыа величин Li и Ci для данных условий, они могут показать общее направление, делающее возможным выбор в определенном частном случае.

Прежде всего рассмотрим влияние величины С на ток инвертора. На рис. 7-11 показан простой фильтр LC с нагрузкой. Пред ставлена индуктивная нагрузка, поскольку это наиболее общий случай. Активными сопротивлениями в реакторе Lx и емкости Ci пренебрегаем.

"It Л

Рис. 7-11. Элементарный фильтр LC с нагрузкой.

/н1 - основная гармоника тока /н - определяется выражением

/n.-Ai.-f/с,.,=. (7-25)

где Zc,i - эквивалентное полное сопротивление для основной гармоники тока пара.плельно включенны.х емкости фильтра п нагрузки;

Zh, = Rn + IXl („)i = I Z„, I (cos у + j sin 4); (7-27)

Ф - угол, определяющий коэффициент мощности нагрузки;

Zc),i=-/ci.i. (7-28)

Положим:

ci. i •

Xa.l=HZml или . = Z =

(7-29)

Подставляя выражения (7-27) и (7-30) в >(7-26), получаем:

- /7Ci (cos у + j sin ч)

Сочетая уравнения (7-31) и (7-25), получаем:

LHi cos у -f / (sin у - Ki)

"=lZ /с. (sin у -/cosy)

Так как

/и. 1/

COS у -f / (sin у - Ki)

iCi (sin <f - / COS V)

(7-31)

(7-32) (7-33) (7-34)

Ha рис. 7-12 локазана зависимость величины - отноше-

ния основной гармоники тока инвертора к соответствующей гармони, ке тока нагрузки от постоянной К\ для различных коэффициентов мощности нагрузки. Из рис. 7-12 видно, что отношение токов инвертора и нагрузки может быть меньше единицы, когда коэффициент мощности -нагрузки отстающий. Векторная диаграмма на рис. 7-13 иллюстрирует это. Как показывает рис 7-13, ток швер-тора будет больше при отключенной нагру.зке, чем под нагрузкой.

Изменение основной гармоники напряжения благодаря фильтру может быть выражено в общем виде как отношение напряжения на нагрузке к напряжению инвертора. На это отнощение оказывают

влияние величины как емкости, так и нндуктивпосгп. Ёмкость К.чме-няет основную гармонику тока, проходящего через реактор, и этот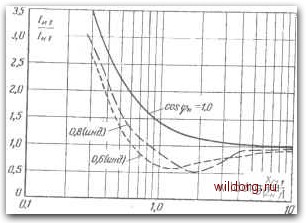

Рис. 7-12. Кривые зависимости тока инвертора от величины емкости фильтра при различных коэффициентах мощности нагрузки, построенные по уравнению (7-34).

ток определяет падение напряжения на зажимах реактора. Основная гармоника напряжения на нагрузки определяется выражением

Примем:

тогда

Хцл = \в11. или Ks = iv-ni

(Ушг

Из уравнения (7-31) получаем:

/С, (sin у-/cosy)

Сочетая (7-37) с (7-39), получаем: Urn

/Ci (sin у - / cos у) cos у-f/(sin у-/С,)

(7-35) (7-36)

(7-37) (7-38)

(7-39) (7-40)

TCi (sin у - / cos о) cos у + j (sin у - /vl)

Lh, Ki (sin у - / cos y) cosy -b у (sin у -л,)

(7-41)

Ha pnc. 7-14 представлено отношение основной гармоники напряжения па нагрузке к основ!юй гар.монике напряжения инвертора в функции кг для ра.чличных значений ki и коэффициента мощности нагрузки. Отметим, что при малых значениях ki и к2 напряжение на нагрузке заметно выше, чем напряжение инвертора. Такие условия иллюстрируются векторной диаграммой на рис. 7-15,а. Для больших значений ki и кг напряжение на нагрузке меньше, чем напряжение инвертора, как показано на рис. 7-15,6.

Желательно также рассмотрсть эффект воздействия величин Z-i и Ct на ослабление гармоник. Эта информация нужна для установления соотношений параметров цепи, требуемых для получения желательного ослабления составляющей данной частоты. Для п-й гармоники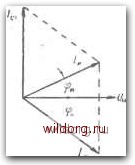

Ll.« = «-L.,i = «HZml (7-42)

(7-43)

Zh„ = i?h -f- ixl („) „ = + ifl („).!,

(7-44)

Рис. 7-13 Векторная

диаграмма простого фильтра LC под нагрузкой, когда ток инвертора растет по мере снижения величины тока нагрузки (1 = 1,0; коэффициент

мощности нагрузки, имеющей индуктивный характер, равен 0,8).

Таким образом,

Опп

/?H = ZHicosy; (н) i= 2н. I Sin у.

= \Zni\ (cos If+ jn sin y):l

M -

zun zo,n-\-jx

чпк2 \Zn,\

zo.n + inkt\zm\ zo.n

--jnk,

15-1503

(7-45)

(7-46)

(7-47)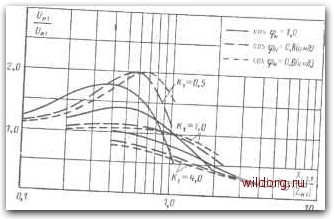

мощное™, построенные по у"раен"„k3°7*4*,T""

-Li---~.

Рис. 7-15. Векторные диаграммы для простого фильтра LC, показывающие, что напряжение инвертора становится меньше, чем напряжение нагрузки при снижении Ai и Kz-

a - Ki-0,6: cos<Pg-=0,8 (инд.); Кг-О.Ъ; б -/Ci-4.0; С08фн-0.8 (инд.); /Са-г.О.

К, = -т

Примем

1 Z,.n fU«n

in IZh.I \0ш\

a, m

где Kj „ - требуемое ослабление амплитуды п-й гармоники. Из схемы рис. 7-11 имеем:

\Zni\ (cos v> + jn sin ?) - / Zh,1 IZhiI (cos <f + jn sin y) -J- (-j -IZh.M - I-J- (cos f + jn sin y)

Zh,I , , . . , .K, •

(cosy-f/Л sinv>) -/-

1 Zo,n

(cos у -f- in sin y)

/ IZh.I

<f + i nsinv -

cos у -j- jn sin v>

(7-48) (7-49)

(7-50)

(7-51)

(7-52)

(7-53)

Подставляя (7-53) и (7-50) в (7-49) и учитывая, что Kz - вещественное число, получаем:

(/Сд„-1). (7-54)

На рис. 7-16 представлено семейство кривых Кг в зависимости От Ki для заданных величин ослабления третьей и пятой гармоник Ка при различных коэффициентах мощности нагрузки. Основная тенденция в этих кривых состоит в том, что с увеличением Kt требуется более высокое значение Лг-

Три семейства кривых на рис. 7-12, 7-14 и 7-16 дают сведения о влиянии основных параметров цепи на работу фильтра. Имеется несколько дополнительных факторов, которые следует рассмотреть, исходя из практических условий, например взаимозависимость номиналов инвертора ш напряжению и яо току с номинальными данными тиристоров, которые могут быть применены. Повышенное напряжение может оказаться более желательным, чем повышенный ток, или наоборот; отсюда - различный технико-экономи-