кривая гфямоугольяой формы имеет посгояилую величину на протяжении всего полупериода анализируемого напряжения. Таким образом, интеграл определяется просто нахождением суммарной площади, ограниченной синусоидальной кривой для дайной гармоники на всем протяжении полупериода основной гармоники-Такая кривая, которая симметрична относительно точки 180°, например простейшая кривая прямоугольной формы, не содержит четных гармоник, за исключением основной синусоиды. Когда такая кривая также симметрична относительно точки 90°. фазы гармоник такие, как они показаны на рис. 7-3 [Л. 7-2]. В общем случае, когда угол сдвига гармоник неизвестен, необходимо произвести операцию, показанную на рис. 7-3 дважды: для основной и для каждой высшей гармоники. Амплитуда данной гармоники определяется как корень квадратный из суммы квадратов двух составляющих, полученных после выполнения двух операций для двух синусоидальных составляющих, сдвинутых по фазе на 90°. Фазы синусоидальных составляющих отноштельно рассматриваемой кривой могут быть выбраны произвольно, чтобы упростить графический анализ.

На рис. 7-4 показано применение упрощенного метода разложения в ряд Фурье для более сложной кривой, которая часто встречается в схемах инверторов. Следовало бы отметить, что не требуется определять интегралы для определенных участков синусоидальной кривой, если ясно, что они будут взаимно погашены, когда будет находиться сумма произведений. Можно заранее установить, например, что четвертая гармоника равна нулю, и что поэтому нет необходимости знать интегралы утасгков синусоидальной кривой для данной гармоники.

Этот упрощенный способ разложения в ряд Фурье абсолютно прост, когда его применяют к «ступенчатым» кривым с формами, показанными на рис. 7-3 и 7-4. Во многих случаях и для более сложных кривых приближенные значения гармоник могут быть получены относительно легко. Если aнaJИзиpyeмaя кривая аппроксимируется горизонтальными участками, то произведения могут быть определены для каждого интервала здременн тем же самым образом, как показано на рис. 7-3 и 7-4. Этот способ также весьма ценен для определения тенденции в изменении состава гармоник при изменении формы рассматриваемой кривой. Важно еще раз подчеркнуть, что этот упрощенный метод является вполне строгим. Однако не требуется производить шаг за шагом математические вычисления для определения гармоник, так как применяется операция графического интегрирования по 1П1тервг1лам.

7-2. ИНВЕРТОРЫ С ВНУТРЕННЕЙ ФИЛЬТРАЦИЕЙ

Последовательный инвертор способен давать напряжение, которое уже без внещнего фильтра близко к синусоиде. Последовательно включенные емкость и индуктивность, необходимые для осуществления коммутации, обеспечивают также и фильтрование. Когда мощность колебательного контура велика относительно мощности, отдаваемой нагрузке, форма кривого напряжения на нагрузке близка к синусоидальной. Как показано в гл. 3, кривая напряжения может значительно отклоняться от синусоидальной, когда схема работает вдали от своей резонансной частоты. При относительно постоянных нагрузке н коэффициенте мощности, 210

а также orpaini4eitiioM диапазоне частоты последовательные инверторы обеспечивают весьма практичный способ генерирования приемлемого синусоидального напряжения.

Фильтрация фактически осуществляется внутри последовательного инвертора. Емкость и индуктивность а инверторе образуют последовательный резонансный контур, который образует высокое сопротивление для гармоник н низкое сопротивление для основной гармоники. Изменение рабочей частоты пе обязательно срывает норд«альную работу схе.мы, но оно меняет состав гармонических в напряжении.

Параллельный инвертор может также осуществлять ощутимую фильтрацию внутри своей схемы. Когда коммутирующая емкость велика, то она вместе с реактором в цепи источника питания может обеспечить достаточную фильтрацию для получения бли:жой к синусоиде кривой напряжения. В этих условиях инвертор имеет относительно большую мощность колебательного контура по сравнению с выходной мощностью.

7-3. ФИЛЬТРЫ [Л. 7-3 и 7-4]

Имеются разнообразные фильтры, с помощью которых можно улучшить кривую выходного напряжения. В данном параграфе рассмотрены фильтры для однофазных инверторов с их обычной прямоугольной формой выходного напряжения.

Назначением фильтра, включенного между инвертором и нагрузкой, является снижение или затухание гармоник, появляющихся в нагрузке. Главный смысл их в том, чтобы обеспечить параллельный путь отвода тока гармоники при наличии последовательного элемента фильтра, на котором выделяются гармоники напря-жепия. Принцип таких устройств показан на рис. 7-5. Затухание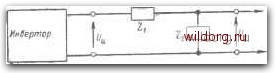

Рис. 7-5. Принципиальная схема внешнего фильтра инвертора. Z, - последовательный элемент фильтра; - параллельный элемент фильтра,

любой данной гармоники зависит от соотношения полного сопротивления параллельной комбинации нагрузки и параллельно включенного элемента фильтра и общего полного сопротивления на этой частоте, т. е.

ZsZb

Св 2„ --

27+27 "" Z, + Zb •

(7-15)

:.„p.S™ V iarpy.™, npoxcmro ...pes нш,.

Основные требования при расчете фильтра для подавления определенных гармоник следующие;

а) сведение к минимуму мощности, потребляемой от инвертора;

б) сведение к минимуму изменений в напряжении на нагрузке, если нагрузка меняется в определенном диапазоне (сведение к минимуму наклона внешней характеристики);

в) максимальное снижение стоимости фильтра;

г) минимальные размеры и вес фильтра.

Однозвенный фильтр LC

Простейшей формой эффективного фильтра является одно звено фильтра LC, показанное на рис. 7-6. В этом фильтре последовательным элементом является индуктивность. Параллельным эле-

Рис. 7-6. Однозвенный фильтр.

ментом - емкость. Передаточная функция для этого ненагруженного илн малонагружеиного фильтра имеет вид;

(7-16)

где Ио - резонансная частота фильтра, а б - декремент затухания.

Отсюда может быть найдена частотная характеристика заменой />=/to, так что получаем:

W со

(7-17)

Обозначая в уравнении (7-17) to/co„ через v, получаем передаточную функцию в нормализованной форме:

0 -v + j2bv-\

(7-18)

Зависимость логарифма величины U-alU-a от относительной частоты, построенная в логарифмическом масштабе, называется логарифмической частотной характеристикой. Частотные характеристики для различных декрементов затухания б показаны иа рнс. 7-7 218

[Л. 7-5]. Заметим, что при малом значении частоты и<1 величина

передаточной функции равна единице log -jj- = log 1 = О .

Степень увеличения затухания по мере повышения частоты сверх У=1,0 приближается к 40 дб на декаду или 12 дб на одну

Рис. 7-7. Усиление фильтра в зависимости от частоты.

Рис 7-8. Фазовый сдвиг фильтра в зависимости от частоты.

восьмую декады. Другими словами при y>I затухание в фильтре возрастает б отношении 4 : 1, когда частота возрастает в отношении 2:1. Как легко видеть, имеется значительный максимум при и=1 и малых величинах б.

Фазовый сдвиг в фильтре в функции частоты показан на рис. 7-8 в тех же са.мы.\ безра.)мсрных координатах, которые

использованы на рис. 7-7. Показаны две кривые для различных величин О. Фазовый сдвиг одного звена фи.тьтра LC равен нулю при

очень малых частотах и при-

Рис. 7-9. Обобщенная схема фильтра LC.

ближается к 180° при высоких частотах.

Рассмотрим передаточную функцию для более полной схемы однозвенното фильтра LC. Этот фильтр показан на рис. 7-9. Потери в реакторе и конденсаторе представлены соответственно активными сопротивлениями Rl и Rl- Предполагается, что нагрузка чисто активная. Передаточная функция равна:

Ry, + R2 +

R,+pL,+

Rn + R,+

R2C,p+ 1

(LrC, + I-p + ( R,Ci + RC, + Ci+)p+l

(7-19)

Так как для эффективного фильтра Ri<Rb и так как хороший конденсатор фильтра имеет весьма малое последовательное сопротивление, т. е. R2<:Rb, то передаточная функция упрощается до вида

(Р) =

R2C,p+ 1

(7-20)

i.C,p + (RiC, + RCi +p+l Сравнивая это соотношение с соотношением (7-16), можно видеть.

"О иСг

R,C, + R,Ci+-;

(7-21) (7-22)

(7-23)

Передаточная функция в зависимости от частоты может быть представлена в виде

/ - + 1

= -т:-7-i:.--тг.-. (7-24)

to* / ti) , со , €0 \

1 . 1 . Rn

Величина «2 обычно весьма велика сравнительно с Wo и другими величинами и, так как в фильтровых конденсаторах R2 весь-

ма мало. Числитель выражения (7-24) /"+1 определяет в основном формы частотной характеристики и характеристики фазового сдвига. Этот множитель сказывается в понижении уровня затухания до 20 дб на декаду и в снижении угла сдвига в сторону отставания до 90° при весьма больших частотах, когда R2 значительно больше Хс. Это иллюстрирует рис. 7-10. Резистор R2 введен в общую схему фильтра LC для того, чтобы проиллюстрировать эффект его воздействия. Обычно этот эффект достаточно мал и им можно пренебречь.

Рис. 7-10. Ослабление фильтра в зависимости от частоты для схемы рис. 7-9.

При индуктивной нагрузке в выражении передаточной функции появляется дополнительный член, зависящий от частоты. Знаменатель выражения (7-20) становится полиномом третьего порядка. При этом анализ фильтра LC с индуктивной нагрузкой существенно усложняется.

Затухание любой синусоидальной составляющей определенной частоты может быть очень легко рассчитано для бо.пьщинства