шнми гармоническими. Общее искажение определяется как корень квадратный из суммы квадратов всех гармонических составляющих. Одним из важных доводов для ограничения искажения гармоническими является нагрев двигателей переменного тока. Гармонические составляющие обычно проявляются в повышенных потерях в двигателе, но не дают увеличения вращающего момента на валу. Во многих измерительных цепях и устройствах может появляться неточность от искажений гармоническими напряження системы переменного тока.

Главное внимание в данной главе уделено рассмотрению различных способов улучшения кривой напряжения инвертора, позволяющих снизить искажения до пределов, требуемых практическими э.пектрическими системами. Применяют разнообразные формы фильтров переменного тока. Однако могут быть применены и некоторые другие схемные решения, обеспечивающие исключение отдельных гармоник или другим путем понижающие общее искажение гармоническими. Контуры LC исполь.уются ие только для обеспечения коммутации в последовательном и параллельном инверторах, но и для фильтрации кривой напряжения нагрузки. Импульсная модуляция, многофазные системы, соответствующие углы сдвига отдельных частей всей системы инверторов и переключение выводов трансформатора снижают гармоники в напряжении импульсно-коммутируемых инверторов.

Выбор практического способа улучшения кривой напряжения инвертора, в том числе выбор типа фильтра, зависит от ряда факторов. Самыми важными из них являются номинальные величины тока и напряжения инвертора, диапазон изменения нагрузки, диапазон рабочей частоты и приемлемое содержание гармонических составляющих. Все эти факторы должны быть тщательно взвешены, что позволяет выбрать самые выгодные решения для данной конкретной системы инвертора.

7-1. ГАРМОНИЧЕСКИЙ АНАЛИЗ КРИВОЙ

Разложение в ряд Фурье [Л. 7-1]

Содержание гармонических может быть определено путем использования разложения в ряд Фурье. Весьма краткое его рассмотрение дано здесь в качестве справочного материала. Любая периодическая функция может быть представлена как бесконечный ряд членов вила

f (х) = -g- а„ -f fli cos x+biSinx-\- ... -f + fl„ cos nx + bnSin nx + ....

(7-1)

где a„. Cl.... , a„, bi, ... . bn являются постоянными коэффициентами которые могут быть определены с помощью следующих выражений:

0,1 = -- f{x)cosnxdx, п = 0. 1,2,...;

(7-2)

Ь„ = - t{x)smnxdx, n=\,2,Ъ,...

Когда разложение придтеняется к кривой напряжения « = f (toi). выражение (7-1) приобретает вид:

+ а„ cos nw( + bn sin (ot + ...,

ц (<ot) = + 5] пЫ + Ьп sin П

.CDt).

(7-4)

где постоянные представляют собой амплитуды п-й гармоники, причем а является постоянной составляющей кривой напряжения. Эти амплитуды определяются выражениями:

ntotdtoC n = 0. 1, 2. 3,...; (7-5)

= -i- j u (toO sin ntatdai; n = 1, 2, 3,...

(7-6)

-Ur,-

Так как кривая выходного напряжения инвертора обычно в основном близка к кривой прямоугольной формы, то в качестве примера определеггия содержания гармонических составляющих возьмем кривую прямоугольной формы. При

кривой прямоугольной формы jpg пря.усугольной

t-lSi

u((Df) выгодно выбрать в качестве начала координат точку

формы.

=0\йган;1ак!чт"о\°;иваГи(.0 -мметрша относительно этой точки, То

Ь„ = 0; п=1. 2....

(7-7)

(7-8) 211

Кривая напряжения прямоугольной формы на рис. 7-1 определяется следующими значениями:

и (tot) = f/„ при О < £( (ы) < -g-;

и (ait) = - t/„ при -g- < u (<«>0 < JC.

(7-9) (7-10)

Подстановка этих соотношени!! в уравнение (7-7) приводит к следующим значениям коэффициентов:

4t/„

а„ = 0; а, = ; fl2 = 0;a, = ; 4 = 0;

«6 = 0; а, =

r4f;,n.

где n - нечетное число.

В этом случае амплитуды гармоник соответствуют определенной закономерности, так что вычисления можно не производить, после того как она найдена. В общем случае, однако, амплитуды должны рассчитываться индивидуально. Количество гармоник, которое .должно быть найдено, зависит от требуемой степени точности в определении общего содержания гармонических составляющих. Возвращаясь к выбранному примеру и подставляя постоянные в уравнение (7-4), мы получаем:

cos U)t

cosSwt , cos5<o< , cos

n(ot \

(7-11)

так как основная гармоника имеет максимальную величину Wmln. Таким образом, в кривой Прямоугольной формы содержатся только нечетные гармоники, амплитуды которых равны амплитуде основной гармоники, деленной на номер дайной гармоники, так что третья гармоника выражается как одна третья амплитуды основной гармоники и т. д.

Упрощенный графический способ разложения в ряд Фурье

К счастью, для многих кривых, вюточая те, которые часто встречаются в инверторах и выпрямителях, гармоники могут быть приближенно определены графически. Это графическое решение является весьма простым способом получения гармоник для кривых определенной формы. В дополнение к этому оно обеспечивает превосходное физическое представление о гармонике и может облегчить понимание эффекта воздействия изменения формы кривой на гармонический состав.

Из уравнений (7-5) и (7-6) вытекает, что амплитуда данной гармоники пропорциональна интегралу произведений мгновенных значенщ"! кривой напряжения на синус (пли косинус) аргумента

„р„ частоте гармоники. Это выражается в форме уравнений еле-дующим образом:

(7-12)

J u(io()sinntotd<u<;

а„~ J ([(toOcos/Kofrfot.

(7-13)

Когда рассматриваемая .ривая «-ь -

ризоитальными Участками в течение вс«с и Р известному

кГл/Д- °гг"""

от учасша синусоидальной кривой составляет.

sin xdx = cosx

1 -cosXi.

(7-14)

Это графически показано на рис. 7-2 для нескольких участков синусоидальной кривой.

Рис 7-2 Пример вычисления интегралов для синусоидальной кривой Интеграл в интерва.пе 0-30 равен

1 - cos 30° 1

}-.Общая 0 15

площадь, ограниченная синусоидальной кривой в течение полупериода, равна 2,0.

Вообще говоря, самое важное, что необходимо знать, это отношение данной гармоники к основной. Оно может быть определено очень просто при использовании этого упроще1Гного графического способа анализа, как это будет проиллюстрировано на двух примерах. Последовательность расчета следующая.

1) Начертить рассматриваемую кривую с амплитудой, равной

единице.

2) Начертить синусоидальную кривую основной частоты с амплитудой, равной единице.

3) Найги сумму произведе1ЩН интегралов от участков основной гармоники на значения ординат кривой на этом участке.

4) Начертить единичную сннусовдальную кривую, соответствующую рассматриваемой гармонике.

5) Найти сумму произведений интегралов участков рассматриваемой гармоники на значения ординат кривой на этом участке.

6) Определить отношение велотины, полученной по п. 5, к величине, полученной по п. 3. Это и будет отношение амплитуды гармоники к амплитуде основной гармоники.

На рис. 7-3 Показано применение этого способа к кривой прямоугольной формы. В аанном случае это весьма просто, так как и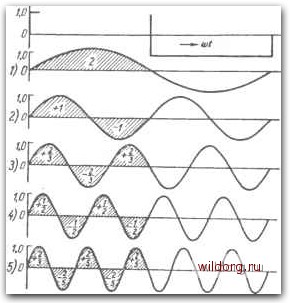

Рис. 7-3. Гармонический анализ кривой прямоугольной формы. / - основная гармоника (сумма произведеннЯ за полупериод основной гармоники равна 2* 1=2); 2 - вторая гармоника (площадь равна половине площади, ограниченной синусоидой основной гармоники, поскольку амплитуды равны, а полупериод в ? раза меньше; сумма произведений за полупериод основной гармоники для второй гармоники равна нулю): 3 -третья гармоника (сумма произведений для третьей гармоники равна 2 2

--•1,0=-; отношение к соответствующей сумме для 2 1 \

основной гармоники "з" " = "з") ~ четвертая гармоника

(сумма произведений за полупериод основной гармоники для четвертой гармоники равна нулю); .5 - пятая гармоника (сумма произведений для пятой гармоники рав-

на-- . 1,0=-; отношение к соответствующей сумме для

основной гармоники равно

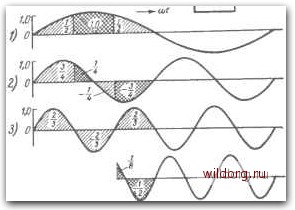
Рис. 7-4. Гармонический анализ многоступенчатой кривой

/ - основная гармоника (сумма произведений за полупериод -1 • 0,5-Ь 1,0 • 1,0 -Ь = Т ) • 2-вторая

с\\1ма произведений за полупериод основной гармоники

гармоники равна гармоника

равна --0,5 -Ь-;-1,0-(-

; 3-третья гар.

сумма произведений за пол\т1ериод оснопной гармоники

2 I V\ 2 1

равна --0,5 + I--g-j-." +-уО.5 = О ; - четвертая гармоника

сумма произведений за полупериод ocHOBnoil гармоники равна f-0.5 +(-i-)-0.5 +(-)-..0 + 1.1.04-1 .0.5+{-L).o.5=0

S-пятая гармоника

[сумма произведений за полупериод основной 1 \ . „ 2

гармоники равна --0.5-1- ( -Тб j"* (~То j*" + Т*

+ (-То + ( -1) •0.5+-"-5 = - отношение

\ I I /3 \ /3 \ 1

ветствующей сумме для основной гармоники равно fjlMfj-s

к соот-