вания (5-127) и (5-81), т. е. после решения трансцендентного уравнения:

/„ + g- = 2 e-<»./2Q)sin<(7r/2<c,,<,:). (5-129)

После определения ti из уравнений (5-81) и (5-82) можно найти величину тока К + а и напряжение Ui в конце интервала 1. Однако эти значения не так важны. Главный интерес представляет собой время to, предоставляемое для восстановления Т1. Достаточно точное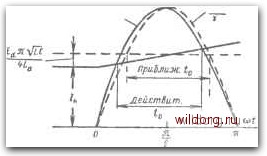

Рис. 5-35. Аппроксимация для расчета времени, предоставленного для восстановления запирающей способности тиристора.

приближение величины to можно получить, заменяя затухающий синусоидальный ток ic [уравнение (5-81)] незатухающей синусоидой, имеющей ту же амплитуду, а линейно возрастающий ток ia [уравнение (5-127)] - постоянным током, равным реальному току в момент времени (л/2)VLC (см. рис. 5-35):

i = /„

Edit /LC

Тогда из рис. 5-35 видно, что

~ 2 l/LC arccos

/н-Ь

2£d X

(5-130) (5-131)

(5-132)

Оптимизация коммутирующей цепи производится подобно тому, как это было описано при выводе формул 156

(5-41) и (5-42), если принять кро.ме этого допущение, что превышение тока над током нагрузки выражается согласно уравнению (5-131).

Интервал 2. Расчетная схема остается той же, что и в режиме холостого хода [рис. 5-30,6], но начальные условия другие. Однако конечное напряжение U4 на емкости С то же, что и раньше [уравнение (5-105)]. Конденсатор С заряжается от t/i - конечного напряжения интервала 1 до ГУг приблизительно постоянным током

Интервал 3. Здесь применима расчетная схема рис. 7-30,е с тем же начальным напряжением на емкости, но начальный ток приблизительно равен hi+I- Как и в случае режима холостого хода, напряжение на емкости колеблется около уровня 2Ei{\ + \IN) с частотой

но амплитуда колебаний получается больше, так как в индуктивности L запасается больше знергии. В обоих основных выражениях для рассеиваемой энергии (5-109) и (5-112) последний член становится ра.вным

-2-/,(/н+/д) Однако как при нагрузке, так и в режиме

холостого хода общие потери энергии в интервалах 1 и 3 равны:

W,-\-W,C[(2EaY~Ut ].

(5-134)

Так как Ui с ростом нагрузки становится меньше, то потери увеличиваются.

Ток во вторичной обмотке дросселя Еа определяется выражением

(5-135)

2NLg

где ток нагрузки ih уменьшается от своего первоначального значения /и. Интервал 3 заканчивается, когда is становится равным нулю и ДЗ закрывается. Из сравнений (5-116) и (5-135) видно, что продолжительность интервала 3 при нагрузке больше, чем в режиме холостого хода, и зависит от тока нагрузки.

Интервал 4. Расчетная Схема подобна представленной на рис. 5-30,г с соответствующими изменениями, вызываемыми появлением тока нагрузки. Напряжение на емкости колеблется около уровня 2Еа с частотой со, а величина рассеиваемой энергии - примерно та же, что и в режиме холостого хода {уравнение (5-120)]. Однако при индуктивной нагрузке колебания продолжаются дольше, чем в режиме холостого хода. Нагрузка имеет большое индуктивное сопротивление при частоте со, и ток нагрузки поддерживает в открытом Состоянии как Т2, так и Д2. Следовательно, эти колебания встречают только дифференциальное сопротивление диода, а не полное прямое падение напряжения. При активной нагрузке колебания затухают быстрее.

Сравнение с предыдущими схемами

Мы проанализировали работу схемы в режиме холостого хода и при индуктивной нагрузке. Но эта, как и другие схемы импульсно-коммутируемых инверторов, может работать и при чисто активной, и при емкостной нагрузке.

Этот инвертор был задуман, как компромисс между двумя схемами, описанными в § 5-1 и 5-4. В нем сделана попытка сочетать лучшие качества и избежать недостатков каждой из предыдущих схем. В частности, цепочка LC, которая дает коммутирующий импульс, действует почти целый полупериод собственной частоты в контуре с малым реактивным сопротивлением, так что большая часть энергии, запасенная в емкости перед коммутацией, возвращается в него обратно после коммутации, и только потери должны пополняться за счет источника питания, как это получается в инверторе, описанном в § 5-1. В схеме § 5-4 в период коммутации значительная часть энергии берется из источника питания. Эта энергия остается запасенной после коммутации, и создает большой циркулирующий ток, проходящий через тиристоры и обратные диоды, пока энергия возвращается обратно в источник питания. Последняя схема запасает меньше энергии и использует лучший способ для ее возвращения. Вообще, чтобы не создавать понижающего к. п. д. обмена энергией между коммутирующими элементами и источником питания, коммутирующий импульс не должен проходить через источник питания. 158

5-6. ВЫСОКОЧАСТОТНЫЙ ИНВЕРТОР

Как было указано во вступлении к этой главе, коммутирующий импульс занимает тем большую долю кал-дого полупериода, чем больше рабочая частота. Наконец, частота может достигнуть такого значения, что следующий коммутирующий импульс будет начинаться сразу после завершения переходного процесса от предыдущей коммутации. При этой частоте те элементы инвертора, которые служат для прекращения или ограничения

Рис. 5-36. Высокочастотный инвертор.

колебаний в коммутирующей цепи в промежутке между следующими друг за другом коммутациями, могут быть опущены. И хотя требуется некоторое воображение, чтобы узнать в этих схемах импульсно-коммутируемые инверторы, тем не менее они имеют подобные последним выходные характеристики.

В качестве примера простого, ио экономичного высокочастотного инвертора на рис. 5-36 показана полумостовая схема. Коммутирующим элементом является простая цепочка LC, включенная параллельно нагрузке. Принцип работы этой схемы иллюстрируется кривыми рис. 5-37. Для упрощения полагаем, что ток нагрузки - отстающий с прямоугольной формой, подобный тому, который получается при фазоуправляемом выпрямителе или при последовательном дросселе насыщения.

Другим вариантом этой схемы является схема со встречно-параллельными вспомогательными тиристорами, включенными последовательно с коммутирующей цепочкой L, С и отпираемыми в том же порядке, как вспомогательные тиристоры в схеме § 5-1. Существенно, чтобы колебания в коммутирующей цепи прерывались вспо-

могательными тиристорами в моменты времени А и В (рис. 5-37), обеспечивая желательную продолжительность полупериода.

Таким образом, получается еще одни тип инвертора со вспомогательно-импульсной коммутацией при ограниченном обратном напряжении, но он менее эффективен,

чем схема в § 5-1, так как коммутирующий импульс проходит через источник питания.

Упрощенную коммутирующую цепочку на рис. 5-36 можно рассматривать также как фильтр, настроенный так, чтобы получить опережающий коэффгщиент мощности общей цепи (нагрузка и LC-цепочка) при рабочей частоте инвертора, и рассчитанный на перекомпенсацию наибольшего отстающего тока нагрузки. В этом случае инвертор всегда имеет опережающий коэффициент мощности, так что ток переключается с тиристора на обратный диод до окончания полупериода (см. рис. 5-37). Следовательно, тиристоры запираются преи<де, чем начинается следующий полупериод отпирания сопряженного тиристора. Выше, в § 5-1 и 5-4, было указано, что при опережающем коэффициенте мощности коммутирующий импульс является излишним.

Вообще инвертор, который питает только емкостную нагрузку, не нуждается в специальных коммутирующих устройствах. В тех случаях, когда для получения опережающего коэффициента мощности применяются фильтры, они могут рассматриваться как коммутирующие цепочки. Более сложные фильтры в дополнение к коммутации могут обеспечивать настройку на определенную гармонику [Л. 5-2]. Однако корректирующий фильтр очень велик, пока рабочая частота недостаточно высока. С этой точки зрения коммутирующая цепочка является 160

Рис. 5-37. Кривые токов и напряжений высокочастотного инвертора (прн 6=60°).

специальным типом фильтра небольшого размера, рассчитанным на получение опережающего тока очень искаженной формы, который «корректирует» коэффициент мощности только в течение коммутационных интервалов.

Анализ коммутирующей цепи

При прямоугольной форме напряжения на нагрузке в схеме рис. 5-36 LC-цепочка потребляет «двугорбый» ток с резко выраженной «впадиной» в момент коммутации, как показано на рис. 5-37. Чтобы сохранить предполагаемую прямоугольную форму напряжения, ток с «провале» /у по величине должен быть равным или больше максимума тока нагрузки /„о. Обозначив собственную угловую частоту и волновое сопротивление цепочки LC через a-lll/LC и Х=-УL/C соответственно, можно применить уравнения (5-7) н (5-12). Начальные условия положительного полупериода:

£=£а f/o = 0. Io = Iv. (5-136)

Тогда уравнения для цепи коммутации в течение положительного полупериода (если пренебречь экспоненциальным затуханием) примут вид:

(5-137) (5-138)

(5-139)

Уравнения (5-137) - (5-139) можно использовать для получения выражений для максимальных напряжений на емкости Ucm и тока 1т, а также тока «в провале» Iv в зависимости от Е, X и 9. Подставляя конечные условия положительного полупериода сй/=соГ/2 = л-Ь26 и ic=-Iv в уравнение (5-137), имеем:

(5-140)

Uc=Ea+XIv sin at-Ea cos at. Как следует из рис. 5-37, иГ=2я-1-4е.

-Л =-%sm2e-/cos2e,

из которого

11-1503

:dge.

(5-141) 161