li LlF"" большим. Напряжение на емкости С в конце интервала 2 можио определить, исходя из (5-102);

(5-104)

(5-105)

Приравнивая правые части уравнений (5-99) и (5-105), получаем трансцендентное уравнение для определения С/г и длительности интервала 2. Приближенное решение его можно получить, полагая в уравнении (5-99), что со/г - малый угол и sin ю/г-со/г.

Таким образом.

с/. ~ 2еа + xlyt, - (2frf - С/,)

(5-106) (5-107)

Из уравнения (5-107) можно видеть, что мы фактически полагаем /д постоянным в течение интервала 2, т. е. что конденсатор заряжается линейно от U\ до С/г. Насколько близка к действительности такая аппроксимация, можно проверить, подсчитав величину ш/г с помощью уравнений (5-107), (5-100), (5-105), (5-97) и (5-92).

со 7,=

-(u/2Q)

(5-108)

0)72 = 0,566 рад, или 32,5° при /V=5; Ld=6L; Q=10. Следовательно, допущение, что co/s мало, вполне приемлемо. 150

Интервал 3. Когда ДЗ находится в проводящем состоянии, ограничивая первичное напряжение трансформатора до 2Ea(\ + \IN), расчетная схема для коммутирующих элементов имеет вид рис. 5-30,в. Начальными условиями интервала 3 являются конечные условия интервала 2 - напряжение на емкости равно С/г в соответствии с (5-105), а ток остается приближенно равным /д [уравнение (5-92)]. Чтобы получить уравнения для

переходного процесса, эти начальные условия должны быть представлены в уравнениях (5-7) и (5-12).

Напряжение на емкости колеблется около 2Еа(\ + \1Щ

с частотой (д=1/уьс. Вообще длительность интервала 3 достаточна для полного затухания этих колебаний. Следует отметить, что ток этих колебаний проходит попеременно через т2 и д2.

Энергия, рассеиваемая этими колебаниями, зависит от разности между начальными и конечными величинами токов и напряжений в элементах

W = -

u,-2e,{l-\-)j+±ul;

(5-109)

-с{2еаг (47)+4-с("У {- ЖУ- (5-110) W, = -Lc (2еаг 0,00007 + С (2) • 0,0156, (5-111)

где величины вычислены для Л/=5; la = l.

Эти потери малы по сравнению с потерями от коммутирующего импульса в интервале 1, которые равны (например, при Q=10):

Г. = с{2еау- -се\--lll ; (5-112)

W,-;-C{2eay\\ --L/ ; (5-113)

W,\c{2eaf-q,21~-\-lll. (5-114)

Напряжение «а первичной обмотке дросселя La в течение интервала 3 равно EaJN, а ток, приведенный к первичной стороне, равен:

(5-11 го

где ip=2ic\ ip,o~2I, a время измеряется от начала интервала 3.

Отсюда вторичный ток

(5-116)

N , Eat

- l£ =!= /Д--

2 2NLa

Интервал 3 кончается, когда становится равным нулю и ЦЗ запирается. Бели положить, что коммутирующий ток ic к этому моменту упал до нуля, то длительность и можно определить из (5-116):

21LaN

Сравнивая (5-117) и (5-86), видим, что:

h = Nti.

(5-117)

(5-118)

Физическая сущность этих результатов состоит в том, что поток в дросселе La, установившийся в интервале 1, спадает до нуля в течение интервала 3. Энергия, запасенная в La, в течение интервала 1 возвращается обратно в течение интервала 3 (за вычетом некоторых потерь).

Интервал 4. После запирания ДЗ расчетная схема снова становится той же, что была в интервале 2, но с другими начальными условиями, показанными на рис. 5-30,г. Напряжение на конденсаторе колеблется около уровня 2Еа, с более низкой частотой сй= = l/j/(L--4Ld)C. Как и в интервале 3, ток колебаний проходит попеременно через Д2 и Т2. Бели выходная частота достаточно мала, то эти колебания затухают до начала следующей коммутации. Энергия, рассеиваемая этими колебаниями,

Г. = -С(2£,)[(1---1) 1]; (5-1,9)

Г-4С(2£,); (5-120)

Г= 1- С{2ЕаУ-0,()А для УУ = 5. (5-121)

Сравнивая уравнения (5-111), (5-114) и (5-121), можно видеть, что большая часть потерь в этом режиме (без нагрузки) возникает в интервалах I и 4, соотношение зависит от величин Q и .V. Пренебрегая относительно малыми потерями в интервалах 2 и 3, можно выразить общую мощность потерь при отсутствии нагрузки и при низкой частоте /:

потерь ~

2I{W, + W,); (5-122)

Р.о..,.=-1С{2ЕаТ\\-е--Ц

(5-123)

/потерь=/С(2£й)2 0,31 для выбранных в нашем примере параметров.

При повышении частоты следующая коммутация наступает прежде, чем в интервале 4 поглотится вся эта энергия.

Начальные условия интервала 1 должны тогда учитывать иные напряжения на емкости С и токи в L и L(j. Анализ усложняется, и результат становится зависимым от частоты. Амплитуда коммутирующего импульса напряжения, генерируемого в интервале 1, может стать выше или ниже, чем при низких частотах. Это делает схему неудобной для работы с регулируемой высокой частотой. Однако при фиксированной частоте схема может быть рассчитана на получение максимального коммутирующего импульса. Теоретическая предельная частота fm получается, когда интервал 4 исчезает. Дальнейшее увеличение частоты привело бы к «вторжению» в интервал 3 периода перемагничивания реактора La-

и<--. (5-124)

При предельной частоте начальное напряжение на емкости равно 2Ed(l + llN), и потери при отсутствии нагрузки приближенно равны:

потерь,. ЫС{2ЕаГ (1,+ / [I -в-"]. (5-125)

noTepb=fmC(2£d)2-0,39 ДЛЯ выбрзнных В нзшем примере параметров.

Таким образом, потери за один период при высокой частоте не сильно отличаются от их значения при низкой частоте. Амплитуда коммутирующего импульса пропорциональна {N+l)/N. Поэтому эта схема применима для достаточно высоких частот, порядка 3 кгц.

Анализ работы схемы при индуктивной нагрузке

На рис. 5-33 и 5-34 показаны кривые напряжений и токов начальной части полупериода. Их полезно сравнить с соответствующими кривыми на рис. 5-31 и 5-32 для холостого хода. Для этого интервала можно допустить, что при малой частоте и сравнительно большой индуктивности нагрузки (по сравнению с Ld) ток нагрузки остается неизменным и равным по величине /н-

Интервал 1. Полагая, что начальное напряжение конденсатора С равно 2Ed, получим расчетную схему коммутационной цепи и начальные условия, соответствующие рис. 5-30,а. Остаются справедливыми уравнения (5-81) и (5-82). Однако начальный ток ip, протекающий через дроссель Ld, обмотку трансформатора OA и Т1, равен току нагрузки /н. В интервале 1 начинают протекать добавочные токи, определяемые (5-83) и (5-84), так что полные токи равны: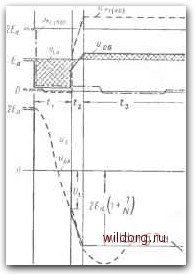

Рис. 5-33. Кривые напряжении (индуктивная нагрузка).

Когда коммутирующий ток ic превышает ia, запирается Т1 и избыточный ток ic-iA начинает протекать через обратный диод Д/. Интервал 1 заканчивается, когда ic снова падает до величины ia, что приводит к запиранию Д/. Время tl может быть найдено путем приравни-154

я и к ь

ш к о.