Типичные для этой схемы формы кривых напряжения на нагрузке показаны на рис. 5-29 для случаев холостого хода и индуктивной нагрузки. В каждом полупериоде выделяются четыре интервала (рис. 5-29). Промежуток, содержащий коммутацию и следующие непосредственно

- «

Рис. 5-29. Кривые напряжений. а - холостой ход: б - индуктивная нагрузка.

за НИМ моменты (интервалы 1, 2 и начало интервала 3) анализируются более подробно. В каждом полупериоде разность между напряжением на нагрузке и э. д. с. источника питания ложится на реактор Ld. При установившихся условиях среднее значение напряжения на реакторе равно нулю, так что среднее за полупериод значение напряления на нагрузке равно Еф

Анализ режима хо.гостого хода

Па рис. 5-27 стрелками пока.-аны принятые за положительные направления токов и напряжений.

Допустим, что к концу нолупериода, в котором тири-

o = a

crop TI открыт, все предыдущие колебания закончились Тогда потенциал средней точки О трансформатора (рис. 5-27) равен i: - потенциалу положительного полюса источника, а та-к как вывод А соединен с отрицательным полюсом Q через Г/, то индуктированное напряжение делает потенциал вывода В равным 2Еа. Конденсатор С заряжен до напряжения 2Еа с отрицательным знаком на выводе А.

Интервал L Открывается тиристор Т2, соединяя точку В с отрицательным полюсом Q. Конденсатор С разряжается через L, Т2 и обратный диод ДЕ Прямое падение Д1 прикладывается к Г/ в качестве обратного напряжения и запирает его. Расчетная схема разряда емкости показана на рис. 5-30,а, с обозначением начальных условий. Стрелками на рис. 5-30,а-г показаны те же условные положительные направления напряжений и токов, что на рис. 5-27.

Подставляя эти начальные условия в уравнения (5-7) и (5-12) получаем приближенные выражения для переходного процесса в виде демпфированных колебаний:

In = C

ir. - -rv~e smcor;

Рис. 5-30. Расчетные схемы для холостого хода (указаны начальные условия).

и - интервал 1: б-интервал 2; е-интервал 3, г - интервал 4.

V LC

(5-82)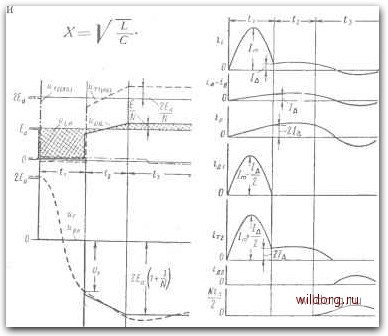

Рис. 5-31. Кривые напряжений. Рис. 5-32. Кривые токов, холо-

холостой ход.

стой ход.

Соответствующие кривые напряжений и токов показаны на рис. 5-31 и 5-32 (интервал ti).

В течение интервала I Т2 и Д1 находятся в проводящем состоянии, поэтому точки А и В, а следовательно и точка О, имеют отрицательный потенциал, равный потенциалу точки Q; трансформатор закорочен, напряжение на выходе равно нулю. Все напряжение источника приложено к индуктивности 1, что определяет линейное возрастание тока:

Этот ток делится пополам между двумя полуобмотками трансформатора:

1 . EJ

1р =

(5-84)

Ток через Т2 равен ic + is, в то время как ток в обратном диоде Д1 равен ic-U- Интервал 1 кончается, когда возрастающий ток ia становится равным коммутационному току ir. iB конце первого полупериода его колебаний. При этом Д1 запирается и расчетная схема изменяется. Если есть величина тока ic и и в конце интервала 1 длительностью (и то из уравнений (5-81) и (5-84) следует:

(5-85)

= е-™ sin о/,;

I Edti

(5-86)

Совместное решение (5-85) и (5-86) должно дать точные значения /д и Л, но они не могут быть получены алгебраически. В первом приближении можно считать:

Подстановка в (5-86) дает:

, ЕйК VLC

(5-87)

(5-88)

Более точное решение можно получить, если заметить, что

sinco/i ==sin (л-co/i) ~я-oti. (5-89)

Подставляя (5-87) и (5-89) в (5-85), получаем:

/, - f е-" (. - со/о = - (- fUC - h). (5-90)

Решая совместно (5-86) и (5-90) относительно /i и , получаем:

(5-91)

/ V EdTi YlC

2La 1

(5-92) (5-93)

Для типичных значений 1 = 61; Q = lO

1,17

1+-2Г

= 0,955.

(5-94)

Таким образом, первое приближение решения (5-87) и (5-88) дает ошибку около 5%. Отношение /д к /,„ - амплитуде коммутирующего тока ic - равно:

Едя У LC

Чтобы определить t/,-напряжение на емкости uc в конце интервала 1, заметим, что

coscu/i = -cos (л-со/,)-1, (5-96)

и, следовательно, из уравнения (5-82)

и, = ~ 2Еае-" cos .4, 2Еае~<\ (5-97)

C/i=2£d-0,855 для Q = 10.

Отметим, что обратное напряжение, приложенное в течение интервала 1 к вспомогательному обратному диоду ДЗ, равно (Л-Ь!).

Обычно Л=5, и номинальное обратное напряжение ДЗ должно быть в 6 раз больше э. д. с. источника питания.

Интервал 2. Диод Д1 запирается, и расчетная схема переходит к виду рис. 5-30,6, где питающее напряжение и индуктивность Ld приведены ко всей первичной обмотке трансформатора и соединены последовательно с коммутирующей цепочкой L, С.

Конечные условия интервала 1 [уравнения (5-92) и (5-97)] являются начальными условиями для интервала 2. Они показаны на рис. 5-30,6. Применяя уравнения (5-7) и (5-12) к новой расчетной схеме, получаем: r2£,-t/,., cos «7

- (mtllQ)

в ; (5-98)

Uc = 2Ea + [XI?.m<t~ ~{2Ea~U,)cos<.4\e-"""\

(5-99)

V(L+ ALa) С

(5-100)

а время / отсчитывается теперь от начала интервала 2. Таким образом, решение снова получается в виде затухающей синусоиды, но с более низкой частотой, чем в интервале 1. При типичном соотношении Ld=6L имеем сй = =Сй/5 и Х=-ЪХ. Напряжение, приложенное к Т1 и ДЕ равно напряжению между точками А и В [см. рис. 5-27 и 5-30,6], которое равно 2Еа минус напряжение на ALa-Так как эти две иоследовательные индуктивности делят напряжение 2£d-«с пропорционально своим значениям, то

ALa + L

(5-101)

Uc + 2Eajr

(5-102)

Отсюда начальный скачок прямого напряжения, приложенного к ТЕ

U. + 2Eajr,

-=2Е,

-. (5-103)

f/Ti,o=2£d-0,860 для(Э=10 и Еа = 6Е

практически равно Ui-начальному напряжению на емкости. Вообще скорость нарастания напряжения должна быть ограничена вспомогательными средствами, чтобы избежать повреждения тиристоров. Это изменит характер переходного процесса между интервалами 1 и 2, но здесь мы не будем этого рассматривать.

Интервал 2 кончается, когда индуктированное во вторичной обмотке дросселя La напряжение становится равным э. д. с. источника питания и ДЗ начинает проводить ток. Это ограничивает дальнейшее повышение напряжения. Потенциал в точке О (и напряжение на нагрузке) устанавливается на уровне Еа{1 + \1Щ, а напряжение на