считать, что ток i становится равным нулю точно в конце каждого полупериода рабочей частоты инвертора, то расчетные формулы для установившегося режима получают следующий вид.

Для промежутка времени, когда тиристор Т1 находится в проводящем состоянии, а тиристор Т2 заперт имеем:

1 - ехр

R \1/2

LC ли

(3-18*)

- Ел

/ R т \ \

Хехр

sin yX/LC-RVAL {t-T/2) {2L,R) y\/LC- RAL J

(3-22)

sin V l/LC - RyAL t 2L

(3-19)

/ R T\l

[-2Г-Т)

LC ALi

sin У l/LC - Ry AL t

(3-20)

Vi/L - RyAL

Для промежутка времени, когда тиристор Т2 находится

в проводящем состоянии, (Tf2<t<T), имеем:

а тиристор Т1 заперт -EJL

[ R Т \-\f \ \1/2

X

(3-21)

* Номера формул, не встречавшихся ранее в этой главе соответ-

чрТу1мТпГГчт*"™ «".веденных в § 3-5. где выполнен расчет схемы рис. 3-1. (Прим. автора.)

( R 1

1 - ехр -22;

Т !

sin Y\ILC-RyAL(t - TI2) {2L/R) V \/LC - RAL J

(3-23)

Ha рис. 3-2 показаны формы кривых напряжения Uc для различных значений 2LIR, причем принято, что YILC-R/iD сохраняется неизменным и равным рабочей частоте иивертора. Когда сопротивление цепи R мало, его изменение «е оказывает ощутимого влияния на резонансную частоту. Для этих условий j?2/4L2«C 1/Z-C, и поэтому резонансная частота схемы l/LC-RjL равна примерно i/ljLC. На рис. 3-2 наибольшая амплитуда кривой имеет место, когда R мало. Если все другие параметры схемы остаются примерно постоянными, то при изменении сопротивления R амплитуда синусоиды постепенно уменьшается.

В тех случаях, когда сопротивление R велико или приближается критическое затухание, а R меняется при неизменном L, необходимо существенно изменять С, чтобы сохранять постоянной резонансную частоту схемы. Это соответствует кривой рис. 3-2 с наименьшей амплитудой.

При критическом затухании R равно 2Хь или 2Хс, что можно показать следующим образом.

,4 = гт, ими 1> =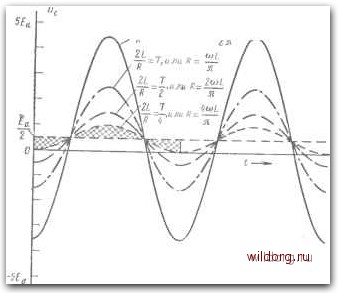

Рис. 3-2. Формы кривых для схемы рис. 3-1. если считать УЧС-ЯУ4!> постоянным и равным частоте инвертора.

Для критического затухания имеем:

R = 2Ly =.2ы,12Х,,

(3-31)

(3-32)

Tmoo = ll\LC равно резонансной частоте в случае RIAU < 1 LC.

И так как

(3-33)

(3-34)

На рис. 3-3 показаны формы кривых для случая, когда 2L/R = T/2 или R = 2(i)L/n.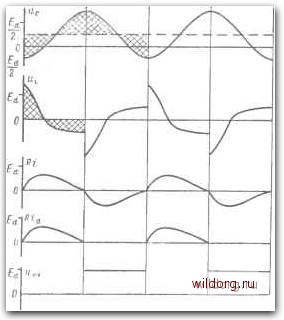

Рис. 3-3. Формы кривых рис. 5-1, если считать V 1 /LC - R/AL постоянным и равным частоте инвертора и 2L/R=T/2 или R = 2ioLJk.

По существу для практических целей очень просто выполнить приближенный расчет схемы, не решая дифференциальных уравнений. Такой расчет базируется на основных принципах работы схемы. Считаем, что тиристоры Т1 и Т2 находятся в проводящем состоянии разные интервалы времени. Напряжение между точкой / и отрицательным полюсом источника постоя1Нного тока на рис. 3-2 имеет величину Еа, когда открыт тиристор Т1, и равно нулю в течение времени, когда открыт тиристор Т2. Таким образом, напряжение, приложенное к последовательной цепочке L, R, С, имеет постоянную составляю-

щую Eal2 II переменную составляюшую прямоугольной формы кривой с максимумом £d/2. При установившемся режиме работы .на зажимах конденсатора может действовать постоянное напряжение, тогда как через конденсатор не может протекать постоянный ток (следовательно, постоянного напряжения не будет и иа зажимах R)\ постоянное напряжение пе может появляться на индуктивности. Кроме того, для случая, когда ток i достигает нулевого значения точно в конце каждого полупериода, не может появляться постоянное напряжение «а индуктивности в течение каждого полупериода (заштрихованные площади кривой рис. 3-3 равны). Переменное напряжение на зажимах нагрузки R можно найти, определив расчетом появляющиеся на зажимах R части основной и каждой гармоник приложенной прямоугольной вол-.ны. Амплитуда основной гармоники приложенной црямо-угольпой волны напряжения с максимумом Edl2 равна:

(3-35)

Действующее значение основной гармоники напряжения на зажимах R равно:

T2"gd 1

Для любой гармоники v2e.

(3-36)

(3-37)

где rt=l, 3, 5, a Уд,- действующие значения отдельных гармоник напряжения на зажимах нагрузки R.

Практически схема рис. 3-1 применяется главным образом для того, чтобы создать приемлемое синусоидальное напряжение на нагрузке. В таких случаях Хь и Хс по существу равны и по величине обычно составляют несколько R. В таких резонансных условиях рабочая частота равна приблизительно l/j/Z-C и форма кривой тока 64

очень близка к синусоиде. Сумма сопротивлений Xl И Хс примерно равна нулю. Поэтому вся основная гармоника приложенного прямоугольного напряжения с максимумом, равным Edl2, оказывается приложенной к сопротивлению нагрузки. Ток нагрузки равен основной гармонике приложенного .напряжения, деленной на сопротивление R. Переменное напряжение на Хс или Х может быть определено умножением этого тока на Хс или Xl. Этот приближенный расчет очень прост и дает достаточно точные результаты прн расчетах для многих встречающихся на практике случаев. Этот метод расчета дает весьма малые ошибки для схем с большим Q.

Схема рис. 3-1 может также работать в тех случаях, когда резонансная частота цепи У [/LC-R/4L больше, чем рабочая частота инвертора. В таком .режиме ток будет достигать нулевого значения и оставаться равным нулю в течение некоторого времени до тех пор, пока не откроется следующий тиристор. Как показано в § 3-5, работа схемы при протекании тока описывается теми же уравнениями (3-18) - (3-23). После того как ток станет равным нулю, напряжение на конденсаторе будет оставаться неизменным, пока не наступит интервал проводимости следующего тиристора. На рис. 3-4 показаны примерные формы крргвых при тех же параметрах, что и на рис. 3-3, но при емкости, в 4 раза меньшей. Резонансная частота цепи возрастает примерно до удвоенного значения рабочей частоты инвертора. Такой режим очень схож с тем, что показано на рис. 3-2 и 3-3, за исключением интервалов задержки, т. е. промежутков времени в течение каждого полупериода, «огда ни один из тиристоров не находится в проводящем состоянии. Такой же режим работы схемы, как на рис. 3-4, будет и в том случае, если частота инвертора снизится, а все остальные параметры схемы сохранятся такими же, как на рис. 3-3. Действительно, при малой частоте инвертора формы кривых будут теми же, что ла рис. 3-3, за исключением интервала задержки в течение каждого полупериода, когда аналогично условиям рис. 3-4 напряжение на конденсаторе остается постоянным.

Приближенный метод расчета может быть также ис-пользован, когда частота инвертора меньше, чем l/ l/LC-R/4L, для промежутка времени, когда один из тиристоров находится в проводящем состоянии. Однако фактические среднеквадратичные токи и напряжения 5-1503 65