Во-вторых, потребуем, чтобы потенциал (5) удовлетворял уравнению (2). Подставив (5) в (2), помножим обе части получившегося равенства на sin ШШ. (pi = 1,2,...) и проинтегрируем по а от О до 0. Учитывая

ортогональность функций sin "" 1d (dRm\

в указанном промежутке, получим

т7Г7

sin-

Rrn{r) =

Amlmir (кг) при Г < а,

ВтКтж (кг) при Г > а.

функция Rm{r) непрерывна при г = го, но ее первая производная по г испытывает при этом скачок

6 = Rmiro + 0) - RUro - 0) = кВтКт (fcro) - кАГщ. (Ы-

Поэтому вторая производная Rmir) будет равна Rm(f) = f>S{i- го).

Подставляя это выражение в (7) и отбрасывая члены, ограниченные при г = Го, получим второе уравнение для определения Л„, S„:

кВпК, (fcro) - kAnln. (fcro) = sin

-0 -J /Зго /3

При упрощении выражений для Л„ и Я„ полезно воспользоваться формулой

K,,{x)lUx)-KUx)I.,{x) = l.

207.

arctg

, « , а - 7 ch -Ь cos

, п а - 7

ch - cos

- дГ arctg

chj+ cos ch-i - cos -

const = -

Virln г( + )

Отсюда видно, что а -> О при г->0и/б<7г;<7->оо при г -> О и /б > тг. В частном случае, когда заряд находится у края плоскости,

209. Поместим заряд q в начале координат, а ось z направим перпендикулярно поверхности пластинки. Тогда уравнения передней и задней поверхностей ее примут вид z = аи z = а-1-е соответственно. Будем искать потенциал в виде

оо оо

<pi=qj Jo(fcri)e-*ll dk+j Ai{k)Jo{kn)e>k (-00 < z < a),

00 00

P2 = jBi{k)Mkri)e-> dk+jB2{k)Jo{kri)e> dk {a < z < b),

= j A2ik)Jo{kri)e~" dk {b < z < 00, rmb = a + e).

} (1)

Граничные условия на поверхностях пластинки дадут систему четырех алгебраических уравнений для определения коэффициентов Ai, А2, Bi, В2.

Ло = \Jrl + + - 2гго cos(7 - а) = \/2гго усЬт? - cos(7 - а),

В!о = у/г + г + - 2гго cos(7 + а) = \/2гго усЬт? - cos(7 + а).

208. сг = const-г \ где 1- расстояние до ребра клина. В частном случае клина, находящегося в поле точечного заряда (см. задачу 205),

Решая эту систему, получим:

g-2feb g-2feo

1 2e-2fe<= 9(1-/6)

2 =9 S2 =

l 2g-2fec

gl-;6)e-2**

l-;62g

!2„-2fec

где;б= 6 = a + c.

Формулы (2) совместно с (1) дают решение нашей задачи. На больших расстояниях за пластинкой {z > 0) поле принимает вид: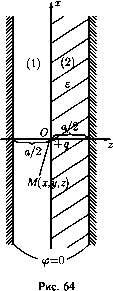

Фиг)

где п

/fT (r?+z2)3/2

-С9-

210. у,(М) = / где п = +у2 (рис. 64).

2д 5?shJfc(o-z)

chfco

Jo(fcri)dfc,

При v/22 + 2

-> О (вблизи заряда) 29

(£ + i)v/;fT

(ср. С задачей 129).

Потенциал (р можно представить в виде

(-1)"

+ K£ooVrl + iz-2an)

Соответствующая система изображений приведена на рис. 666.

211. Можно ввести бисферические координаты так, чтобы поверхности внутренней и внешней обкладок были координатными поверхностями = и = 2 соответственно. Для этого нужно провести ось z через центры обкладок так, как это показано на рис. 65. Координаты центров обкладок будут при этом равны zi=a cth , Z2 = а cth 2 (а - параметр би-сферических кооодинат). Радиусы обкладок связаны с величинами а, 2