159. Обозначим поверхности внутренней и внешней сфер соответственно через 5i и 52 и положим потенциал внешней сферы равным нулю. Удобно решать задачу в сферической системе координат с полярной осью, направленной вдоль линии, соединяющей центры сфер, и с началом координат в центре внутренней сферы(рис. 62). В этих координатах уравнение поверхности Si запишется в виде г = о. Чтобы получить уравнение поверхности 52, заметим, что из треугольника 00А следует:

i = 1 - (1)

Ь у/В? + (? -2cRcosd

Из (1) с точностью до членов первого порядка по с находим уравнение поверхности 52:

i?(i?) = b + cPi(cosj9), (2)

Pi (cos I?) = cos j9.

Член cPi(cosj9) = ccosj? в (2) описывает отклонение от сферической симметрии, которое обращается в нуль при с -» 0. Естественно искать потенциал в виде разложения по сферическим гармоникам (см. приложение 2), ограничившись первыми двумя членами. При этом второй член, учитывающий отклонение от сферической симметрии, должен быть пропорционален с.

Итак, положим

ф, д) = (Ai + )+ с(А2Г + ) cost?, (3)

где Аг и Bi определяются из граничных условий:

dSi =

Окончательно:

Отсюда плотность заряда на внутренней сфере:

Я 39С .

сила, действующая на внутреннюю сферу:

63-аЗ-

160. АС =

а О С

161. При увеличении заряда q на dq энергия U его взаимодействия с шаром возрастет на dU = ipdq, где ip - потешщал индущфованных на шаре зарядов. Но этот потенциал сам пропорционален q: ip = const • q.

Поэтому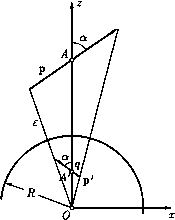

U = jdU=q=\ipq.

Если бы величина ip не зависела от q (потенциал внешнего поля), то энергия взаимодействия была бы вдвое больше {U = = ipq). Используя (1) и результаты задачи 153, получим

откуда

Рис. 63

1«. с/ = Й-

и = -

F = -

2£(о2-Д2)

£(о2 - Д2)2

Qq qR\2a - R) ea ea\a - R

В случае одноименных зарядов Qq > о, и сила взаимодействия может обратиться в нуль, а при достаточно больших q или малых расстояниях а - даже стать отрицательной (притяжение).

163. Пробный заряд q должен быть мал по сравнению с зарядами, расположенными на других проводниках и дюлектриках, и не должен находиться слишком близко к местам неоднородности среды, например, к границам проводников и диэлектриков, чтобы обратное влияние зарядов, наводимых пробным телом, было мало. Например, при измерении электрического поля заряженного проводящего шара нужно, чтобы сила электрического

§ 1. Основные понятия и методы электростатики 279

изображения была мала по сравнению с измеряемой силой Щ- (Q - заряд

шара, а - расстояние от пробного заряда до центра шара). Это приводит к условию (см. ответ предыдущей задачи)

Q i2a/R-ir

{a/R){a/R-ir

которое выполняется только при не слишком малых a/R и не слишком больших q/Q.

164. Изображением электрического диполя р=р(еа; sinа+вгcosa) в заземленном шаре является система, состоящая из точечного заряда q =

= cosa и диполя р = p(y) sina + ег cosa), находящихся в точ-ке а (рис. 63) на расстоянии г = от центра шара. р2Д(г2со82а + Д2)

2£(г2 - Д2)3

= -4 [(2г + R) cos2 а + ЗД21,

£(г2 - Д2)4

рДг81п2а

"2£(г2-Д2)3

в предельном случае г R получим, полагая г = R + z, R оо, z = const, результаты задачи 148 (диполь у проводящей плоскости).

165. ст =--?cosj9,

где I? - угол между р и направлением из центра в точку наблюдения. Индуцированные заряды создают в полости однородное поле Е =

166. Силы, действующие на неоднородность, могут быть получены дифференцированием величины

U = Y4mQlrn (1)

при постоянных Qf.