526. В прямоугольный волновод с идеально проводящими стенками вносится ферродголектрическая пластинка толщиной d < о, намагниченная вдоль оси волновода (рис. 32). Пользуясь формулой, полученной в предыдущей задаче, определить с точностью до членов порядка d изменение Ак постоянной распространения волны типа Ню- Диэлектрическая проницаемость пластинки - скалярная величина, тензор ее магнитной проницаемости приведен в условии задачи 435.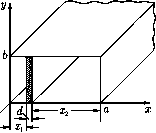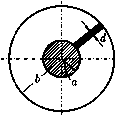

Рис. 32

Рис. 33

527. В коаксиальный волновод (рис. 33) вставлена тонкая феррито-вая пластина {d < а, Ь), намагниченная вдоль оси волновода. Определить изменение АА; постоянной распространения поперечной электромагнитной волны.

УКАЗАНИЕ. Амплитуды возмущенных полей определить таким же методом, как в предыдущей задаче.

528. Рещить предыдущую задачу для случая, когда постоянное под-магничивающее поле Щ направлено перпендикулярно оси волновода. Рассмотреть два направления этого поля: а) Но перпендикулярно щирокой грани пластинки; б) Щ перпендикулярно узкой грани пластинки.

529. Определить типы собственных колебаний в полом резонаторе с идеально проводящими стенками. Резонатор имеет форму прямоугольного параллелепипеда, его размеры ахЬ х h.

530. Определить число собственных колебаний AN{u>), приходящихся на интервал частот Да; в полом резонаторе обьема V, рассмотренном в предыдущей задаче. Считать, что выполняются неравенства Да; >С w и ДАТ > 1.

531. Резонатор имеет форму прямого кругового цилиндра высотой h и радиуса о. Считая стенки резонатора идеально проводящими, найти частоты собственных колебаний. Рассмотреть колебаш1я электрического и магнитного типов.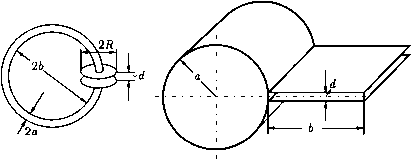

Рис. 34

Рис. 35

532. Две круглые металлические пластинки радиуса R находятся на малом расстоянии d друг от друга, образуя конденсатор. Обкладки конденсатора замкнуты проводником толщиной 2о, имеющим форму кольца радиуса Ь (рис. 34). Найти собственную частоту колебаний такого «открытого резонатора», предполагая применимым квазистационарное приближение. Все проводники считать идеально проводящими.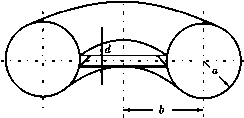

Рис. 36

533. Найти собственную частоту колебаний системы, изображенной на рис. 35, предполагая, что соответствующая ей длина волны Ао велика

по сравнению с размерами системы. Потерями энергии и краевыми эффектами пренебречь.

534. Для уменьшения потерь энергии на излучение вместо открытого колебательного контура (см. рис. 34) используют закрытый резонатор, со-стояший из соединенных вместе тороидальной камеры и плоского конденсатора с круглыми пластинами (его разрез и размеры показаны на рис. 36). Найти собственную частоту uiq основного типа колебаний такого резонатора в квазистационарном приближении. При каких условиях применимо такое приближение? Стенки резонатора считать идеально проводяшими.

535. Решить предыдущую задачу для тороидального резонатора с камерой прямоугольного сечения (рис. 37).

536. Резонатор представляет собой цилиндр кругового сечения (внутренний радиус 6, высота h), вдоль оси которого вставлен идеально проводящий стержень радиуса а (рис. 38). Стенки цилиндра также обладают идеальной проводимостью. Между стержнем и одним из торцов цилиндра оставлен зазор d. Найти собственные частоты поперечных относительно оси системы электромагнитных колебаний, считая, что длина волны этих колебаний много больше зазора d (но не высоты h цилиндра). Как изменится спектр колебаний при d -> О?

-26 2а

Рис. 37

Рис. 38

537. Известны собственные частоты колебаний и собственные функции Е,, Н, резонатора с идеально проводящими стенками. Вычислить изменение собственных частот, вызванное конечной проводимостью стенок резонатора. Поверхностный импеданс С стенок мал.