Определение шаровых функции приведено в приложении 2.

4. Доказать, что если а» = Tikbk в каждой системе координат и Тгк - тензор II ранга, а bfe - вектор, то - тоже вектор.

5. Доказать, что есть тензор II ранга.

6. Доказать, что если Tjfe - тензор II ранга и Pjfe - псевдотензор

II ранга, то TikPik - псевдоскаляр.

7. Показать, что симметрия тензора есть свойство, инвариантное относительно вращении, т. е. тензор, симметричный (антисимметричный) в некоторой системе отсчета, остается симметричным (антисимметричным) и во всех системах, повернутых относительно исходной.

8. Показать, что если тензор Sik - симметричный, а тензор Aik - антисимметричный, то AikSik = 0.

9. Доказать, что сумма диагональных компонент тензора II ранга является инвариантом.

10*. В некоторых случаях бывает удобно вместо декартовых компонент вектора ах, Су, рассматривать его циклические компоненты, определяемые формулами а±1 = Т(ах ± idy), «о = «г- Выразить скалярное

И векторное произведения двух векторов через их циклические компоненты. Выразить также циклические компоненты радиуса-вектора через шаровые функции Лежандра.

11*. Найти компоненты тензора e~i, обратного тензору eik. Рассмотреть, в частности, случай, когда eik является симметричным тензором, заданным в главных осях.

12. Пусть во всех координатных системах компоненты вектора а линейно выражаются через компоненты вектора Ь: а, = eikbk- Доказать, что совокупность величин etk является тензором II ранга. (Точнее, etk является тензором, если а и b - оба полярные векторы или псевдовекторы, и псевдотензором, если один из векторов - полярный, а другой - аксиальный.)

13. Показать, что совокупность величин AikiBik, где Aiki - тензор

III ранга, а Bik - тензор II ранга, является вектором.

14. Найти закон преобразования совокупности обьемных интегралов Тгк = / XiXkdV при пространственных поворотах и отражениях (Xi и Xfe - декартовы координаты).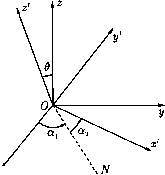

15. Составить матрицы преобразования базисных ортов: при переходе от декартовых координат к сферическим и обратно; при переходе от декартовых координат к цилиндрическим и обратно.

16. Записать матрицу преобразования компонент вектора: при отражении трех координатных осей; при повороте декартовой системы координат вокруг оси z на угол а.

17. Найти матрицу преобразования компонент вектора при повороте координатных осей, определяемом углами Эйлера ai, 6, «2 (рис. 1), путем перемножения матриц, соответствующих поворотам вокруг оси z на угол ai, вокруг линии узлов ON на угол в и вокруг оси z на угол «2.

18. Найти матрицу £)(ai0a2), с помо- "х щью которой преобразуются циклические

компоненты вектора (см. задачу 10*) при Рис. 1

повороте координатной системы, определяемом углами Эйлера а\, в, а2 (рис. 1).

19*. Показать, что матрица бесконечно малого поворота системы координат а может быть записана в виде а = Ц-£, где е - антисимметричная матрица {etk = -еы)- Выяснить геометрический смысл etk-

20. Доказать, что если а - ортогональная матрица преобразования, то при ее транспонировании получается матрица обратного преобразования.

21. Показать, что матрица преобразования базиса координатной системы при отражении или повороте и матрица преобразования компонент вектора совпадают.

22*. Доказать, что при поворотах или отражениях четного числа координатных осей определитель преобразования равен -Ы, а при отражениях нечетного числа координатных осей этот определитель равен -1.

23. Показать, что если в некоторой системе координат соответствующие компоненты двух векторов пропорциональны, то они пропорциональны в любой другой системе координат. (Такие векторы называются параллельными.)

Преобразования, определитель которых равен +1, называются собственными; преобразования с определителем -1 - несобственными.

24*. Во всех декартовых системах координат задана совокупность величин еца, обладающих следуюощми свойствами: при перестановке любых двух индексов eiki меняет знак; ei23 = 1-

Показать, что эта совокупность вгы образует псевдотензор III ранга (совершенно антисимметричный единичный псевдотензор III ранга).

25. Доказать, что компоненты антисимметричного тензора II ранга при вращениях преобразуются как компоненты вектора.

26. Записать выражения для компонент векторного произведения двух векторов и вихря вектора с помоп0>ю тензора еш. Указать, как преобразуются эти величины при вращениях и отражениях.

27. Доказать равенства:

а) eikieimn = <5iro<5fcn - <5m<5fcro;

б) eikieklm = 2<Jim-

28. Записать в инвариантной векторной форме:

а) einieiraeimpeatpanarbmCt,

б) einiekraeimpestpOranbkbiCtC.

29. Показать, что Ткафк - Tikakh = 2ш • {а х Ь), где Тгк - произвольный тензор II ранга, а и b - векторы, ш - вектор, эквивалентный антисимметричной части Тк-

30. Представить произведение [а • (Ь х с)] [а • (Ь х с)] в виде суммы членов, содержащих только скалярные произведения векторов.

Указание. Применить теорему об умножении определителей или воспользоваться псевдотензором III ранга dki (см. задачу 24*).

31*. Показать, что единственным вектором, компоненты которого одинаковы во всех системах координат, является нулевой вектор; что всякий тензор II ранга, компоненты которого одинаковы во всех системах координат, пропорционален Sik, тензор III ранга - eiki; тензор IV ранга - {SikSim +

+ kmhl + 5ц5кт)-

32*. Пусть п - единичный вектор, все направления которого в пространстве равновероятны. Найти средние значения его компонент и их произведений: щ, щпк, щпкЩ, щпкЩПт, пользуясь трансформационным свойством искомых величин, а не прямым вычислением соответствующих интегралов.

33. Найти усредненные по всем направлениям значения следующих выражений: (а • n), (а • п)(Ь • п), (а • п)п, (а х n), (ах п)-(Ь х п), (а • п)(Ь • п)(с • n)(d • п), если п - единичный вектор, все направления которого равновероятны, а, Ь, с и d - постоянные векторы.