энергетических уровней, сколько элементарных ячеек содержит кристалл. Сделаем здесь еще один важный вывод, заключающийся в том, что каждое электронное состояние в 1фисталле необходимо нумеровать двумя квантовыми числами: волновым вектором к или, что все равно, квантовым числом Z, и номером энергетической зоны п. Например, (ркп{г). Причем волновой вектор мы рассматриваем в схеме приведеппых зон, т. е. в первой зоне Бриллюэна.

На модели Кронига-Пенни можно очень наглядно проследить, как квантовые числа приближения свободных электронов (Р = 0) переходят в квантовые числа, описывающие вырожденные энергетические состояния электронов в изолироваппых атомах.

Рассмотрим под каким углом кривая зависимости энергии от волнового вектора внутри каждой зоны пересекает ее границу. Имеем уравнение Кропига-Пепин:

/(/За) = cos(fca).

Дифференцируем его по /За, т. е. по энергии:

; = -sin(fca)f. а /За ар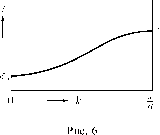

На каждой границе зоны, как видно из рис. 5, ка = птт, отсюда sin ка = 0.

df d3

Поскольку -- Ф о, то необходимо, чтобы - = 0. Имеем:

с1ва dk

й2 dk de

так как

"20, то

dk= при к = п-.

(7.28)

Это значит, что дисперсиоппая кривая пересекает границу зоны под прямым углом, что также весьма важно и носит совершенно общий характер. На рис. 6 приводится качественно дисперсионная зависимость е{к) при п = 1,

т. е. для первой зоны Бриллюэна. При к = имеем 4 = 0. Основной

особенностью приближения Кронига-Пенни является то обстоятельство, что оно позволяет па основе одной схемы рассмотреть различные случаи

одноэлектронных приближений, различающиеся энергией связи электрона. Все выводы этого приближения носят всеобщий характер, утверждающий зонную структуру энергетического спектра электрона в периодическом поле решетки. В дальнейшем мы еще вернемся к приближению Кронига-Пенни в связи с изучением локальных электронных состояний в металлах.

Лекция 8

8.1. Методы расчета энергетической зонной структуры

Рассмотренные ранее приближения позволили выяснить основную осо-беппость энергетического спектра электронов в металлах - его зонную структуру. Мы условились в связи с этим каждому электронному состоянию сопоставлять два квантовых числа: волновой вектор к в первой зоне Бриллюэна и номер энергетической зоны п. Нам известно, что в каждой зоне имеется определенное число состояний, равное числу значений волнового вектора в первой зоне Бриллюэна, т. е. числу элементарных ячеек в кристалле. Каждое состояние может быть заполнено, согласно принципу Паули, двумя электронами с противоположными спинами. Нам необходимо зиать, в какой последовательности располагаются энергетические зоны, каков закон дисперсии внутри каждой зоны, какова ширина разрешенной и запрещенной зоны энергии, какова плотность состояний в области энергий, подвержеппых тепловому возбуждению и т. д.

Расчеты зонной энергетической структуры металлов, призванные ответить на эти вопросы, образуют область весьма тонких вычислительных методов, которые в настоящее время хорошо освоены. На саму зонную структуру большое влияние оказывает симметрия зон Бриллюэна и ячейки кристаллической решетки, поэтому для расчетов таких структур характерно использование теории групп. Она позволяет заметно упростить, а иногда и уточнить расчеты, так как в точках высокой симметрии исходные одноэлек-тронпые уравнения Шредингера значительно упрощаются.

Число методов, использующихся при расчетах структуры энергетических ЗОИ, достаточно велико. Однако, мы рассмотрим только наиболее важные из них, применяемые при расчетах зон в металлах. Наше рассмотрение будет сводиться к решению одноэлектронного уравнения Шредингера, считая, что эффективный кристаллический потенциал (стр. 61) известен.