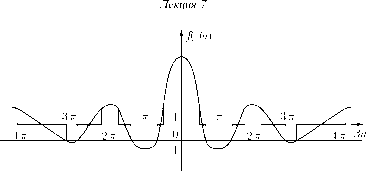Рис. 5

параллельные оси /За, находим точки пересечения прямых с кривой, описываемой функцией /. Эти точки и есть решения трансцендентного уравнения (7.18). При этом видно, что там, где / > 1, вещественных корней пет. Это значит, что значения /За, соответствующие / > 1, а значит и энергии, не являются в этих интервалах собственными энергиями в уравнении Шредингера (7.2). Следовательно, весь интервал изменения /За, а значит и е, является дискретным, т. е. распадается на зоны разрешенных и запрещенных энергий и значений /За. Разрешенные значения /За на рис. 5 показаны жирной чертой. С возрастанием /За ширина разрешенных значений /За, а значит и энергий, растет за счет уменьшения запрещенных. Каждому разрешенному значению энергии соответствует два значения /За, отличающиеся знаком. Следовательно, приближение Кронига-Пенни дает нам тот же результат, что и приближение почти свободных электронов, т. е., спектр энергий электрона в периодическом ноле решетки состоит из непрерывных полос, разделенных интервалами запрещенных значений энергии. Равноценность выводов обоих приближений позволяет утверждать, что распад энергетического спектра на полосы в приближении Кронига-Пенни не связан с принятыми предельными условиями. Обсуждая уравнение Кронига-Пенни, мы не делали никаких заключений о величине приведенного обрезывающего потенциала. Однако энергетический спектр электрона существенно зависит от этой величины. Предположим, что Р = О, тогда, согласно (7.18) ,

cos(fca) = cos(/3a),

(7.19)

и, следовательно, ±ка + 2ттп = /За. Это значит, что /За может принимать

любые значения, т. е. разрешенными являются все значения энергии то нуля до бесконечности. Такая ситуация, как мы знаем, свойственна свободным электронам, когда энергетический спектр непрерывен и отсутствуют интервалы запрещенных энергий.

Предположим другой крайний случай, т. е. Р = оо. Мы знаем, что если величина Р растет, то, согласно рис. 5, зоны дозволенных значений /За уменьшаются и когда Р = оо эти зоны вырождаются в дискретные уровни. Действительно, если внимательно изучить рис. 5, то легко увидеть, что в этом предельном случае величина /За вообще не зависит от к, а определяется соотношением

/За = птт, где гг = ±1, ±2, ... . (7.20)

или, раскрывая значение /3, находим

£» = гг = ±1, ±2, ... . (7.21)

Как известно, эта формула определяет энергетические уровни электрона в изолированном атоме. Следовательно, этот случай соответствует полностью связанному электрону. Сопоставляя оба предельных случая, можно сказать, что величина обрезывающего приведенного потенциала Р характеризует энергию связи электрона, т. е. его свободу или локализацию.

Рассмотрим еще случай, когда величина Р сравнительно велика и электроны сильно связаны. Зоны дозволенных энергий тесно примыкают к значениям /За, равным тт. Пусть ширина этих зон есть А, тогда разрешенные значения (За можно задать так:

/За = ггтг + А, где А и 0. (7.22)

Подставляем это условие сильно связанных электронов в уравнение Кро-нига-Пенни:

cos(afc) = (-1)" + РА. (7.23)

Действительно, так как

cos(/3a) = cos(n7r + А) = cos(n7r) cos А + sin(n7r) sin A = (-1)", sin(/3a) = sin(n7r + A) = sin(n7r) cos A + cos(n7r) sin A = (-1)"A, /За = ггтг + A ~ ггтг.

тг Р

[(-l)"cos(/ca) - 1].

Отсюда, используя (7.22), находим

/За = ггтг + А = ггтг < 1

-[(-l)"cos(fca)-l] (7.24)

Раскрывая величину /3, согласно (7.8), находим в явной форме энергетиче-

ский спектр сильно связанных электронов:

2ша Г9

cos(fca) ,

l-j, + j,{-ircos{ka) п=±1,±2, ... .

(7.25)

Из этой формулы очень наглядно видны особенности энергетического спектра сильно связанных электронов.

Потребуем, далее, чтобы рассматриваемая кристаллическая цепочка удовлетворяла циклическим условиям Борна - Кармана, т. е. перейдем от безграничного к ограниченному кристаллу. Мы знаем, что в этом случае волновой вектор меняется не непрерывным, а дискретным образом согласно формуле (5.30)

2TVZ Na

где Z - целое число, изменяющееся, согласно (5.31), в интервале

(7.26)

(7.27)

Каждому значению z из этого интервала будет соответствовать два решения, т. е. когда /3 > О и когда /3 < 0. Однако на каждое значение волнового вектора к приходится строго один энергетический уровень в каждой энергетической зоне. Следовательно, можно повторить и здесь уже известное нам положение (стр. 71), что каждая энергетическая полоса содержит столько

Разрешаем уравнение (7.23) относительно ширины разрешенной зоны: