Eg/2=Elf±{UgU.gy . (6.13)

Итак, на границе зоны Бриллюэна энергия электрона в периодическом поле решетки имеет два значения:

Eg/2=El-{UgU.g) , (6.14)

Eg/2=El + {UgUg)K (6.15)

т. е. меньше и больше соответствующего значения энергии свободного электрона £д/2- значения энергии разделены энергетической «щелью», шириной 2{UgUg). Можно сказать, что при значениях волнового вектора, близких к границе зоны Бриллюэна, происходит отклонение закона дисперсии от квадратичного, причем это происходит за счет смешивания электронных состояний, различающихся на вектор обратной решетки. Это смешивание приводит к понижению энергии одного состояния и повышению энергии другого состояния и на границе зоны возникает разрыв энергетической кривой. Значения энергии, попадающие в этот разрыв, не могут быть собственными энергиями электронных состояний в кристалле и составляют запрещенную энергетическую зону. Это и есть основной результат, характерный для электронов в периодическом поле. Он утверждает, что в металле энергетический спектр (закон дисперсии) носит зонную структуру, т. е. обратное пространство состоит из отдельных полос разрешенных и неразрешенных энергий, чередующихся между собой. Для всех значений волнового вектора к, лежащих внутри зоны Бриллюэна, энергия является непрерывной функцией вектора к. Эта непрерывная совокупность значений энергии и представляет энергетическую полосу. В схеме приведенных зон (рис. 2) энергия становится многозначной функцией волнового вектора. Отметим еще раз, что разрывность энергетического спектра электрона в периодическом поле является фундаментальным свойством, обуславливающим многие свойства металлов. Наличие запрещенной энергетической зоны означает, что в кристалле не может возникнуть электронных волн с энергией, лежащей в этой зоне. Если пучек электронов с энергией, соответствующей запрещенному значению, падает на кристалл, то он весь должен быть отражен, поскольку электроны с такой энергией не могут двигаться в кристалле. Таким образом, любая попытка возбудить электронные волны

с энергией, лежащей внутри запрещенной зоны, не приводит к возникновению стационарного состояния, а введенное возмущение быстро затухает. Природа возникающей особенности в энергетическом спектре электронов заключается в осуществлении условия (6.3):

к -к= Gn,

(6.16)

которое соответствует плоскости в обратном пространстве, где образуется энергетический разрыв. Это условие по-существу является одной из форм записи известного закона отражения Брегга-Вульфа

пХ = 2(isin.

(6.17)

Следовательно, можно сказать, что зонная структура энергетического спектра является следствием брэгговского отражения электронов от решетки. В трехмерном случае качественная картина одномерной задачи сохраняется полностью, однако, ширина запрещенной зоны не всегда соответствует таковой в одномерной модели. В зависимости от характера периодического потенциала может возникать наложение соседних разрешенных зон. Рассмотрим для примера двумерную квадратную решетку в обратном пространстве (рис. 3). Пока волновой вектор к электрона близок к центру зоны Бриллюэна мы имеем концентрическую окружность для изоэнергетической линии; затем по мере увеличения энергии изолиния \ энергии коснется границы зоны Бриллюэна и потеряет окружную форму. Дальнейшее увеличение энергии соответствует появлению линий равной энергии в других зонах Бриллюэна, причем на границе зоны происходит разрыв непрерывности изолиний энергии, т. е. эти изолинии как бы отражаются от границы зоны.

Сформулируем теперь кратко основные результаты рассмотренной задачи о состояниях электронного газа в периодическом поле:

1. Энергетический спектр электрона в периодическом поле дискретен, и, следовательно, для электронных состояний в металле характерна зонная энергетическая структура.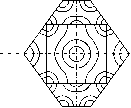

Рис. 3

6.1.1. Оператор Блоха в представлении операторов вторичного квантования

Представляет интерес некоторые предыдущие рассуждения о состояниях электрона в периодическом поле перевести на язык операторов вторичного квантования. Этот переход очень привлекателен в связи со своей компактностью записи.

Прежде всего получим многочастичный оператор Блоха, суммируя од-ноэлектронные операторы (5.4):

Каждому одноэлектронному оператору Блоха соответствует собственная волновая функция Блоха

9Jfc(r) = exp(«fc r)Mfc(r). (6.19)

Построив соответствующие полевые операторы ч/+(г) и %p{r), согласно (3.27) и (3.28), можно записать в представлении чисел заполнения one-

2. Внутри каждой энергетической зоны зависимость энергии от волнового вектора является непрерывной функцией, причем отклонение от квадратичного закона существенно только для состояний вблизи границы зоны Бриллюэна.

3. Ширина запрещенной энергетической зоны связана с Фурье-образом периодического потенциала и в одномерном случае равна 2{UgUgY/.

4. Природа возникающей особенности в энергетическом спектре заключается в осуществлении брэгговского отражения электронов от решетки.

5. Собственные волновые функции оператора Блоха представляют собой смешение плоских волн, отличающихся на вектора обратной решетки с различным весовым множителем.

6. Качественные результаты одномерной модели справедливы и в многомерном случае.