/„2 \

\2™ У

Е сые» = EkY с,„е* (6.6)

Для полного решения задачи необходимо определить значение коэффициентов Cfc„. Для этого выберем из разложения (5.27) функцию

Скп ехр{-г{к + G„) • г),

соответствуюш;ую определенному значению вектора обратной решетки и умножим ее на уравнение (6.6), интегрируя по всему объему кристалла:

+ Y.CknCkn [и{г)е---УЧг =

= EkJ2cknCkn 1 e-(=+«-)"-e»(=+«")--d3r.

Поскольку функции Блоха образуют ортонормированную систему, то можно предыдуш;ее выражение переписать так:

я п •

= -Efc СкпСкп Snn,

CknCknEk+Gn - СкпСкпЕк + Скп CknUn-n = 0.

Знак суммы в первых двух членах этого выражения пропадает. Un - фурье-образ потенциала U{r). Итак, имеем:

Скп (Ek+Gn - Ек) = - CknUn-n- (6.7)

Запишем уравнение Шредингера (5.5), подставляя выражение функции (5.27):

Придавая векторам G„ и G„/ конкретные значения, получаем систему уравнений относительно коэффициентов Скп разложения функции Блоха. Когда коэффициенты найдены, то все электронные состояния определены. Нас будут интересовать только те значения вектора обратной решетки, которые лежат в первой зоне Бриллюэна, т. е. всего два значения для случая одномерной решетки:

= -5,

(6.8)

Это соответствует центру и границе зоны Бриллюэна. Итак, подставляя (6.8) в систему уравнений (6.7), находим

Ck,i{El-Ek)+Ck,-gUg = Q,

Ck,-g {El g-Ek)+Ck,0U-g=0.

(6.9)

Эта запись означает, что среди совокупности коэффициентов Ск, п мы выделили только два коэффициента, соответствующие волновым функциям, описывающим электронные состояния вблизи центра зоны Бриллюэна и ее границы. Смесь этих волновых функций и будет соответствовать состояниям электрона в периодическом поле. Рассмотрим явно систему (6.9). Условием разрешимости ее является равенство нулю детерминанта

det =

Ek-Ek и-а

EU-Ek

= О,

El Ek {El + El g) + ElEl g UgUg = 0.

Таким образом, для энергии возмущенного периодическим полем электронного состояния имеем:

преобразуем это выражение:

Ек = \ {El + El g) ± \{El - El gf + 4С7,С7 ,

(6.10)

Здесь очень хорошо видно, что в результате возмущения, обусловленного периодическим потенциалом, исчезают, как самостоятельные, электронные состояния с энергией Е, -д

е2 =

(6.11)

а вместо них возникает смешанное состояние с энергией Ек (6.10), которому соответствуют смешанные волновые функции. Еще раз подчеркнем, что возникшее состояние с энергией Ек явилось результатом смешивания из-за возмущения двух ранее вырожденных по энергии невозмущенных состояний. Рассмотрим подробнее выражение для энергетического спектра (6.10) электрона. Определим обратную решетку для одномерной ионной цепочки и зависимость энергии от волнового вектора невозмущенного состояния Е (6.11) в схеме приведенных зон (рис. 2). Далее, рассмотрим два случая: Пусть волновой вектор к принимает значения близкие к центру зоны Бриллюэна fc и О, тогда оказывается, что разность невозмущенных энергий Е - Е д велика в сравнении с возмущающим потенциалом Ug (по условию задачи он мал) и, согласно выражению (6.10), имеем:

к-\ [к + Ек-д ± {Е - Ek-g]

Здесь необходимо выбрать знак (+), иначе мы не будем в центре зоны Бриллюэна: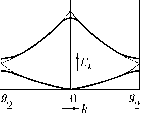

Рис. 2

Ек - Е1 =

(6.12)

Это значит, что в центре зоны Бриллюэна электроны в периодическом поле тождественны свободным электронам и им отвечает квадратичное дисперсионное соотношение. Далее, рассмотрим состояние с волновым вектором к, лежащим иа границе зоны Бриллюэна, т. е. к = д/2. Подставляем значение к в (6.10):

Ек =

19/2

E%/±2iUgUgy