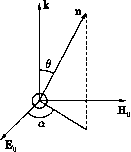Рис. 85

458. Дипольные моменты шара запишутся в виде

Р = /ЗеЕое

-гы*

m = /3„Ное

-tut

где /Зе и 0т - электрическая и магнитная поляризуемости шара, которые в общем случае являются комплексными величинами.

По формулам (XII. 17) и (XII.20), приведенным в гл. XII, найдем компоненты векторов ЕиН рассеянной волны:

На = Ев =

(00080 +0т) cosa,

Не = -Еа =

и?Ео

(/3e + /3m)sina.

Углы 0 и а, характеризующие направление рассеяния, указаны на рис. 85.

Дифференциальное сечение рассеяния определяется по формуле (VIII.26):

das(Q,a)

459.

dasie)

[/Зe(cos 0cos2 а + sin а)+

+ /3„ (cos в sir? а + cos а) + {0,0;, + 010т) cos в[

dasie,a) + das(e,a+)

2с4 Втгш

{\0ef + /3m)(l + cosв) + 2{0,0*„, + 010т)cose] dn,

as = {\0e\ + \0mn

Чтобы определить степень деполяризации рассеянного излучения, нужно найти главные направления тензора поляризации. В рассматриваемой задаче это легко сделать из соображений симметрии. При фиксированных к и п (см. рис. 85) выделенными направлениями для Eq будут направление нормали к плоскости рассеяния и направление в плоскости рассеяния, перпендикулярное к.

460. Для дюлектрического шара:

/3„COS0 + /3e

(Tan =

2с4 (1Т) +

Для идеально проводящего шара:

das пр = [5(1 + cos2 в)-8 cos в] dQ,

107Ri£V /l-2cosg\2

tr.np- , Рпр- 2-COS0 )

Из формулы для daea видно, что сечение рассеяния дюлектрическим шаром симметрично относительно направлений вперед {в = 0)и назад {в =

= 7г). Отношение = 1. Сечение рассеяния проводящим шаром зна-аа-8д(7г)

. rfa-enp(O) 1

чительно более анизотропно и несимметрично: --=7- = . Свет, рассе-

d(Ts пр(7Г) У

янный дюлектрическим шаром под углом в = , будет полностью поляризованным; при рассеянии идеально проводящим шаром полная поляризация достигается при cosd = , в = = 60°.

Применение полученных формул в случае диэлектрического шара законно, если можно пренебречь эффектами, связанными с конечной скоростью распространения электромагнитной волны внутри шара, т. е. если

Этим направлениям поляризации соответствуют дифференциальные сечения рассеяния dcTs(9, и dcTs{e,0), полученные при решении предыдушей задачи. Степень деполяризации р определяется как отношение меньшей из этих величин к большей.

Если \13т\ < /Зе,Т0

d(Tsie,0) /Зт + /3е cos в

длина волны внутри шара велика по сравнению с его радиусом. В случае идеально проводящего шара, распространения волны внутри шара не происходит, и достаточно, чтобы выполнялось условие о <С А, где А - длина волны в веществе, окружающем шар.

461. Так же, как и в задаче 458, нужно рассмотреть излучение индущфованных электрического р и магнитного m моментов. Выберем систему координат, как показано на рис. 86. Вектор к первичной волны лежит в плоскости xz. Рассмотрим два случая поляризации падающей волны: а) вектор Eq лежит в плоскости падения xz; б) вектор Ео нормален к плоскости падения.

В случае а) компонента внешнего электрического поля, продольная относительно плоскости диска: Ео = -Eqx = Eocosa; поперечная компонента: Eq± = -Eqz = Eq sin a. Электрический момент p в рассматриваемом приближении (о <С А) можно вычислить как статический момент проводящего диска в однородном электрическом поле.

Согласно результатам задач 197, 199, продольная поляризуемость диска: /Зе = а поперечная поляризуемость: 0е± = 0. Поэтому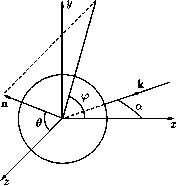

Рис. 86

Рх = 0е\\Еох = --0 cosa, py=pz = 0.

Магнитное поле имеет только продольную составляющую. Но продольная магнитная поляризуемость диска равна нулю (см. задачу 390), поэтому m = 0.

Дифференциальное сечение рассеяния

dcTs = cos2 q(1 - sin 1? cos у?) dQ.

Полное сечение рассеяния

«т. =

128Л;4 „„„2 277гс

cos а.