
 |
|
Главная страница Электростатика проводников [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [ 103 ] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] [167] [168] [169] [170] [171] [172] [173] [174] [175] [176] [177] [178] [179] [180] [181] [182] [183] [184] [185] [186] [187] [188] [189] [190] [191] [192] [193] [194] [195] [196] [197] [198] [199] [200] [201] [202] [203] [204] [205] [206] [207] [208] [209] [210] Постоянное магнитное поле Для прямоугольного сечения L = 2iV2/iln 26+а 26-а 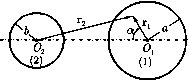 Рис. 70 При 6 » а опять имеем = АжпЗ. Если ток течет непосредственно по оболочке тора, то самоиндукция уменьшается в раз по сравнению с самоиндукцией тора, обмотанного проводом. В соответствии с этим будем иметь: L = 47г(6 - л/62 д2) для тора круглого сечения и 26-1-а L = 2h\n 2b-а для тора прямоугольного сечения. 270. Вычислим магнитную энергию единицы длины линии по формуле (V.16). Векторный потенциал прямого провода с током был получен в задаче 242. Для провода 1 (рис. 70) запишем его в виде Aiz = C- при Г1 < а, Au=C-(l + 2\n при Г1>а. Векторный потенциал, создаваемый проводом 2, получится при замене в (1) J на -J, а на 6 и п на Г2. Находим магнитную энергию: Интегралы, входяшие в (2), можно вычислить, использовав формулу (3.765) из справочника [90]. Учитывая затем связь между коэффициентом индуктивности и магнитной энергией системы, получим окончательно: .Sf = 1 + 21п. 271. Полная магнитная энергия тока, протекающего по проводнику, складывается из двух частей: W = Wi + W2, (1) - энергия, запасенная внутри проводника и интегрирование ведется по обьему проводника, - энергия, запасенная в остальном пространстве. Предположим, что можно ввести параметр го, имеющий размерность длины и удовлетворяющий условию а < Го < Д, (2) где а - радиус проводника, R - радиус кривизны осевой линии проводника (который в общем случае меняется от точки к точке). Тогда на расстояниях, меньших Го, магнитное поле можно считать совпадающим с полем бесконечного прямого провода. В частности, внутри провода: (см. задачу 242). Это позволяет найти «внутреннюю» энергию W\: W. = i. (3) Для определения «внешней» энергии W2 построим вспомогательную поверхность 5, опирающуюся на произвольный контур, лежащий на поверхности проводника, и введем скалярный потешщал ф. Скалярный потешщал будет испытывать на S скачок ф-ф = Щ.. (4) Интеграл, через который выражается W2, можно преобразовать следующим образом: jiB-H)dV = - JBgiaAdV = - j div(VB) dV = - фВ dS (здесь опущен индекс 2 и использовано уравнение div В = 0). В последнем интеграле интегрирование должно проводиться по обеим сторонам вспомогательной поверхности 5 и по поверхности проводника S (см. рис. 71, на котором изображено сечение проводника некоторой плоскостью). Интеграл по бесконечно удаленной поверхности обращается в нуль вследствие конечных размеров проводника с током. Таким образом, Первый из этих интегралов обращается в нуль, так как в силу условия (2) магнитное поле на поверхности S совпадает с полем прямолинейного провода и имеет, следовательно, только касательную составляющую. Для преобразования других двух интегралов нужно использовать равенство (4) и условие непрерывности компоненты Д„. Получим На больших расстояниях от провода (г > го) магнитное поле не зависит от распределения тока по сечению проводника, поэтому можно считать, что ток течет по оси. На малых расстояниях (а < г < Го) это поле совпадает с магнитным полем бесконечного круглого щшиндра, и тоже можно считать, что ток течет по оси. Таким образом, интеграл в формуле (6) представляет собою поток магнитной ин-дукщш, создаваемой током, текущим по оси проводника, через поверхность, которая опирается на замкнутый контур, лежащий на поверхности проводника. Используя выражение потока через коэффициент взаимной индукции (V.22), получим 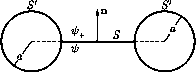 Рис. 71 С помощью формул (1), (3), (7), используя связь между коэффициентом самоиндукции и магнитной энергией системы, получим требуемую формулу для коэффициента самоиндукции: [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [ 103 ] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] [167] [168] [169] [170] [171] [172] [173] [174] [175] [176] [177] [178] [179] [180] [181] [182] [183] [184] [185] [186] [187] [188] [189] [190] [191] [192] [193] [194] [195] [196] [197] [198] [199] [200] [201] [202] [203] [204] [205] [206] [207] [208] [209] [210] 0.0149 |