244. Я. = -М(агсЬе + агсЬе),

Ну = -йУп) I Я. = 0.

Ось у перпендикулярна полосе и проходит через ее середину.

245. Пластины отталкиваются с силой

, 4J?2/ а 1., а2 + б2\

246. Az = -flnri = ln; + %+jl,

И - Mi - аху

" ду с rlrV

тг dAz 2Jfa-x , а + х\

Координаты проводников с током в перпендикулярной к ним плоскости равны (а, 0) для тока +J и (-а, 0) для тока -J; п и гг - расстояния от точек (а, 0) и (-а, 0) до точки наблюдения.

247. а) Между плоскостями Я = г, в остальном пространстве Я=0;

б) между плоскостями Я = О, в остальном пространстве Я = г. В обоих случаях магнитное поле направлено перпендикулярно току и параллельно токонесущим плоскостям.

243. При г < а

Az = Ci, В = 0;

при а < г < 6 при г > 6

>1г = -1п + Сз, = "3.

Остальные компоненты А и В равны нулю. Две любые константы, входящие в Az, можно выразить через третью, использовав условия непрерывности векторного потешщала на границах.

248. Я„ =

c(b-a)

, Нх = Hz = 0; ось у нормальна к плоскости.

проведенной через оси цилиндров.

249. В цилиндрической системе координат, ось z которой перпендикулярна плоскости кольца и проходит через его центр,

= (f) [(1 - - 1т], Az = A. = 0,

где К{к) и Е{к) - полные эллиптические интегралы Лежандра, к" =

4аг

Компоненты магнитного поля:

Нг =

Hz =

2J Z

v/(a + r)2 + 22l На оси витка (г = 0) эти выражения переходят в

27ra2j?

Яа =0.

Нг = 0, Hz =

c(a2 + z2)3/2-

250. В любом сечении такой трубки поток индукции будет один и тот же. Поэтому уравнение поверхности трубки:

= JBdS = f{r, z) = const,

где поверхность интегрирования S представляет собою круг радиуса г в плоскости, перпендикулярной оси симметрии (центр круга лежит на оси симметрии). Так как Аа не зависит от а, то с помощью теоремы Стокса получим

j B-dS = A-dl = 2тггАа{г, z) = const.

Линии пересечения этих поверхностей с плоскостями а = const и дают искомые линии магнитной индукции.

251. Компоненты магнитного поля: (-1)"

дф у. (-1)" „(2„). ./rf" „ Г2 ,

H.---j-H >iz)[) -Hz--H iz) + ...,

n=0

Ha = 0.

Векторный потенциал выражается через напряженность магнитного поля с помопц>ю теоремы Стокса и соотношения Н = rot А:

- - ,2п+1

= Шг)-...

252. Hz = (cos 01+cos $2),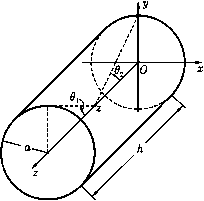

где (см. рис. 68): cos 01 =

у/а + {h- 2)2

cos 02 =

Va2 + 22

253. Решим задачу методом векторного потенциала. Плотность поверхностного тока, возникающего при вращении сферы.

1 = е,

"47га

sint?

p (полярная ось выбрана вдоль векто-

ра ш). Векторный потенциал во всех точках, не лежащих на поверхности сферы, удовлетворяет уравнению Лапласа. Как следует из симметрии системы, векторный потенциал можно выбрать так, чтобы была отлична от нуля только компонента Аа, которая не будет зависеть от угла а. Поэтому уравнение для векторного потенциала запишется:

Аа=0

(см. ответ к задаче 47).