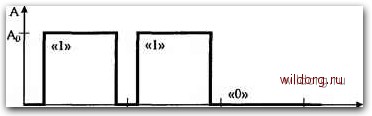ti t2 ta t t

Рис. 1.3. Сигнал с прямоугольным представляющим параметром (передается значение 110)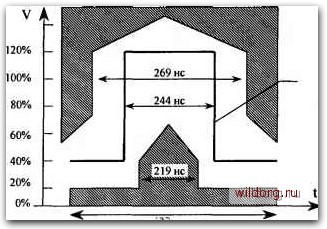

Номинальный импульс

488 нс

Рис. 1.4. Шаблон импульса (Рекомендащ1я G.703 МККТТ)

В определении цифровой коммутации ничего не говорится об операциях над цифровым сигналом, т.е. не вводятся ограничения на такие операции. Единственным условием является сохранение при коммутации цифровой формы сигнала, однако, при этом используемая форма представляющего параметра не оговаривается.

В большинстве случаев первичные сигналы систем электросвязи не приспособлены для непосредственной передачи по линиям, для чего они в общем случае подвергаются модуляции. Модуляция - это преобразование одного сигнала в другой путем изменения параметров сигнала-переносчика в соответствии с преобразуемым сигналом. В качестве сигнала-переносчика используют гармонические сигналы, периодические последовательности импульсов и т.д.

В других случаях вместо модуляции используют другие специальные преобразования. Например, при передаче по линии цифрового сигнала двоичным кодом может появиться постоянная составляющая сигнала за счет преобладания единиц во всех кодовых словах. Отсутствие же постоянной составляющей в линии позволяет использовать согласующие трансформаторы в линейных устройствах, а также обеспечить дистанционное питание регенераторов постоянным током. Чтобы избавиться от нежелательной постоянной составляющей цифрового сигнала, перед посылкой в линию двоичные сигналы преобразуются с помощью специальных кодов. Для первичной цифровой системы передачи (ЦСП) принят код HDB3.

Кодирование двоичного сигнала в модифицированный квазитроичный сигнал с использованием кода HDB3 производится по следующим правилам (рис. 1.5).

О i i i

0000000000

0 0 0 0 1 1

0 0 0 0

+ B 0

-B

Рис. 1.5. Двоичный и соответствующий ему HDB3 коды

1. Сигнал кода является квазитроичным. Три состояния его обозначаются как +В, -В и 0.

2. Пробелы (нули) двоичного сигнала кодируются в сигнале кода пробелами (нулями). Однако для последовательности из 4 пробелов применяются специальные правила (см. п.4).

3. Импульсы (единицы) двоичного сигнала кодируются в сигнале кода попеременно как +В и -В (чередование полярности импульсов). При кодировании последовательности из 4-х пробелов вводятся нарушения в правила чередования полярности импульсов (см. п.4).

4. Последовательность из 4-х пробелов в двоичном сигнале кодируется следующим образом:

а) первый пробел этой последовательности кодируется как пробел, если предыдущий импульс сигнала кода имеет полярность, противоположную полярности предшествующего нарушения чередования полярностей, и сам импульс не является нарушением чередования полярностей, и как импульс (т.е. + В или -В), если предшествующий импульс сигнала кода имеет такую же полярность, как предшествующее нарушение чередования полярностей, или сам этот импульс является нарушением чередования полярностей. Это правило обеспечивает попеременную инверсию следующих друг за другом нарушений чередования полярностей, с тем чтобы не вводить постоянную составляющую;

б) второй и третий пробелы всегда кодируются пробелами;

в) последний из 4-х пробелов всегда кодируется, как импульс, полярность которого такова, что она нарушает правило чередования полярностей.

1.3. Импульсно-кодовая модуляция

Преобразование непрерывного первичного аналогового сигнала в цифровой код называется импульсно-кодовой модуляцией (ИКМ). В телекоммуникациях в качестве основания кода выбрана двоичная последовательность, реализуемая с наименьшими аппаратными затратами. Основными операциями при ИКМ являются операции дискретизации по времени, квантования (дискретизации по уровню дискретного по времени сигнала) и кодирования.

Дискретизацией аналогового сигнала по времени называется преобразование, при котором представляющий параметр аналогового сигнала задается совокупностью его значений в дискретные моменты времени, или, другими словами, при котором из непрерывного аналогового сигнала с(1) (рис. 1.6, а) получают выборочные значения с„ (рис. 1.6, б). Значения представляющего параметра сигнала, полученные в результате операции дискретизации по времени, называются отсчетами.

Наибольшее распространение получили цифровые системы передачи, в которых применяется равномерная дискретизация аналогового сигнала (отсчеты этого сигнала производятся через одинаковые интервалы времени). При равномерной дискретизации используются понятия: интервал дискретизации At (интервал времени между двумя соседними отсчетами дискретного сигнала) и частота дискретизации (величина, обратная интервалу

дискретизации). Величина интервала дискретизации выбирается в соответствии с теоремой Котельникова.

Согласно теореме Котельникова, аналоговый сигнал с ограниченным спектром и бесконечным интервалом наблюдения можно без ошибок восстановить из дискретного сигнала, полученного дискретизацией исходного аналогового сигнала, если частота дискретизации в два раза больше максимальной частоты спектра аналогового сигнала:

Технически дискретизация по времени производится стробированием сигнала c(t) ключевым элементом, замыкающимся через интервал дискретизации на малое время t«A

Как указывалось ранее, канал тональной частоты (основной канал аналогового телефонного канала) должен занимать полосу 300...3400 Гц. Следовательно, частота дискретизации должна быть не менее: fd= 2x3400 = 6800 Гц.

Согласно рекомендациям Международного консультативного комитета по телефонии и телеграфии (МККТТ) для сигнала, передаваемого по каналу тональной частоты, принята частота дискретизации /\)=8000 Гц. Такая частота облегчает реализацию фильтров аппаратуры ЦСП.

При квантовании (рис. 1.6, в) отсчеты с„ ряда Котельникова, принимающие в реальных условиях значения в диапазоне от с„,„ до с„ах (динамический диапазон сигнала), аппроксимируются одним значением из конечного числа значений yi...y„, называемых уровнями квантования. Такая операция подобна округлению и приводит к погрешности, называемой шумом квантования.

Выбор уровней производится таким образом, чтобы, с одной стороны - минимизировать шумы квантования, с другой стороны - упростить реализацию квантователя. Наиболее просто квантователь реализуется при равномерном квантовании, уровни которого расположены в диапазоне с„/„- c„„ с шагом А. Квантованные значения отсчета могут выбираться в соответствии со следующим правилом: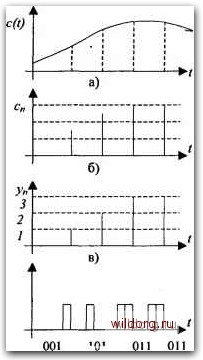

101 г)

Рис. 1.6. Принцип ИКМ

если

если

У,+Мс,<у,

Разность между действительным и выбранным значениями и будет шумом квантования, абсолютная величина которого не превышает А/2.

Уменьшение шума квантования прямым способом (Д -> 0) приводит к большому числу уровней квантования и, как следствие, к необходимости передавать кодовые слова большой длины, что приводит к необходимости увеличения скорости передачи цифрового потока.

Можно показать строго математически, что равномерное квантование не приводит к минимально возможной среднеквадратичной величине погрешности шума квантования (малый сигнал имеет большое значение шума квантования и наоборот). Теоретически мож-